Wave Equation

import numpy as np
import matplotlib.pyplot as plt
from IPython.display import HTML
from matplotlib.animation import FuncAnimation

The wave equation is given by

\[ \frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2} \ , \ \ 0 \leq x \leq L \ , \ \ t \geq 0 \ , \ \ c \in \mathbb{R} \]

Initial and Boundary Conditions

The wave equation is second order with respect to time \(t\) therefore we need two initial conditions to specifiy a unique solution. The initial conditions are functions \(f(x)\) and \(g(x)\) which determine the solution and derivative at time \(t=0\):

\[ u(x,0) = f(x) \ \ \ \text{and} \ \ \ u_t(x,0) = g(x) \]

Dirichlet boundary conditions specify the values of the solution at the endpoints:

\[ u(0,t) = A_0 \ \ \ \text{and} \ \ \ u(L,t) = A_L \]

Neumann boundary conditions specify the values of the derivative of the solution at the endpoints:

\[ u_x(0,t) = Q_0 \ \ \ \text{and} \ \ \ u_x(L,t) = Q_L \]

When one endpoint is a Dirichlet boundary condition and the other is a Neumann boundary condition then we call them mixed boundary conditions. For example:

\[ u(0,t) = A_0 \ \ \ \text{and} \ \ \ u_x(L,t) = Q_L \]

Discretization

Choose the number of steps \(N\) in the \(x\) direction and the number of steps \(K\) in the \(t\) direction. These choices determine the step sizes \(\Delta x\) and \(\Delta t\), and create a grid of points:

\[\begin{split} \begin{align} x_n &= n \Delta x \ , \ \ n = 0,1, \dots, N \ , \ \ \Delta x = \frac{L}{N} \\ t_k &= k \Delta t \ , \ \ k = 0,1, \dots, K \ , \ \ \Delta t = \frac{t_f}{K} \end{align} \end{split}\]

Here we have chosen some final time value \(t_f\) so that the domain of the solution \(u(x,t)\) is a finite rectangle \([0,L] \times [0,t_f]\). The goal of a finite difference method is to compute the matrix

\[ U = [u_{n,k}] \]

which gives approximations of the solution \(u(x,t)\) at the grid points:

\[ u_{n,k} \approx u(x_n,t_k) = u(n \Delta x,k \Delta t) \]

where \(x_0 = 0\), \(x_N = L\), \(t_0 = 0\) and \(t_K = t_f\).

Central Time Central Space

Apply the central difference formula for \(u_{tt}\) at position \(x_n\) and time \(t_k\)

\[\begin{split} \begin{align*} u_{tt}(x_n,t_k) &= \frac{u(x_n,t_{k+1}) - 2 u(x_n,t_k) + u(x_n,t_{k-1})}{(\Delta t)^2} + O((\Delta t)^2) \\ &= \frac{u_{n,k+1} - 2 u_{n,k} + u_{n,k-1}}{(\Delta t)^2} + O((\Delta t)^2) \end{align*} \end{split}\]

Apply the central difference formula for \(u_{xx}\) at position \(x_n\) and time \(t_k\)

\[\begin{split} \begin{align*} u_{xx}(x_n,t_k) &= \frac{u(x_{n+1},t_k) - 2u(x_n,t_k) + u(x_{n-1},t_k)}{(\Delta x)^2} + O \left( (\Delta x)^2 \right) \\ &= \frac{u_{n+1,k} - 2u_{n,k} + u_{n-1,k}}{(\Delta x)^2} + O \left( (\Delta x)^2 \right) \end{align*} \end{split}\]

Plug the formulas into the wave equation at position \(x_n\) and time \(t_k\)

\[\begin{split} \begin{align*} u_{tt}(x_n,t_k) &= c^2 u_{xx}(x_n,t_k) \\ \frac{u_{n,k+1} - 2 u_{n,k} + u_{n,k-1}}{(\Delta t)^2} &= c^2 \left( \frac{u_{n+1,k} - 2u_{n,k} + u_{n-1,k}}{(\Delta x)^2} \right) \end{align*} \end{split}\]

Rearrange to solve for \(u_{n,k+1}\)

\[ u_{n,k+1} = r^2 u_{n-1,k} + 2(1 - r^2) u_{n,k} + r^2 u_{n+1,k} - u_{n,k-1} \ \ , \ \ r = \frac{c \Delta t}{\Delta x} \]

This is the central-time-central-space (CTCS) finite difference method for the wave equation.

CTCS with Dirichlet BCs

Matrix Equations

Consider Dirichlet boundary conditions \(u(0,t) = A_0\) and \(u(L,t) = A_L\). Write out the CTCS equations:

\[\begin{split} \begin{array}{cccccccccccccccc} u_{0,k+1} & = & 2u_{0,k} & & & & & & & & & & & - & u_{0,k-1} \\ u_{1,k+1} & = & r^2 u_{0,k} & + & 2(1 - r^2) u_{1,k} & + & r^2 u_{2,k} & & & & & & & - & u_{1,k-1} \\ u_{2,k+1} & = & & & r^2 u_{1,k} & + & 2(1 - r^2) u_{2,k} & + & r^2 u_{3,k} & & & & & - & u_{2,k-1} \\ & \vdots & & & & & & \ddots & & & & & & \vdots & \\ u_{N-2,k+1} & = & & & & & r^2 u_{N-3,k} & + & 2(1 - r^2) u_{N-2,k} & + & r^2 u_{N-1,k} & & & - & u_{N-2,k-1} \\ u_{N-1,k+1} & = & & & & & & & r^2 u_{N-2,k} & + & 2(1 - r^2) u_{N-1,k} & + & r^2 u_{N,k} & - & u_{N-1,k-1} \\ u_{N,k+1} & = & & & & & & & & & & & 2u_{N,k} & - & u_{N,k-1} \end{array} \end{split}\]

Note that we are writing the boundary conditions in a particular way:

\[ u_{0,k+1} = 2u_{0,k} - u_{0,k-1} \]

\[ u_{N,k+1} = 2u_{N,k} - u_{N,k-1} \]

so that the full vector of values at time index \(k-1\) appear in the last column.

These finite difference equations show us that approximations at time \(t_{k+1}\) are given by matrix multiplication of the vector of approximations at time \(t_k\) along with the vector at time \(t_{k-1}\). Therefore we can write the CTCS method as an iterative matrix formula

\[ \boldsymbol{u}_{k+1} = A \boldsymbol{u}_k - \boldsymbol{u}_{k-1} \]

where

\[\begin{split} A = \left[ \begin{array}{ccccccc} 2 & & & & & \\ r^2 & 2(1 - r^2) & r^2 & & & & \\ & r^2 & 2(1 - r^2) & r^2 & & & \\ & & & \ddots & & & \\ & & & r^2 & 2(1 - r^2) & r^2 & \\ & & & & r^2 & 2(1 - r^2) & r^2 \\ & & & & & & 2 \end{array} \right] \end{split}\]

\[\begin{split} \boldsymbol{u}_k = \begin{bmatrix} u_{0,k} \\ u_{1,k} \\ \vdots \\ u_{N-1,k} \\ u_{N,k} \end{bmatrix} \hspace{20mm} r = \frac{c \Delta t}{\Delta x} \end{split}\]

The finite difference formula at \(k=0\) yields

\[ u_{n,1} = r^2 u_{n-1,0} + 2(1 - r^2) u_{n,0} + r^2 u_{n+1,0} - u_{n,-1} \]

with the “ghost value” \(u_{n,-1}\). Use the initial condition \(u_t(x,0) = g(x)\) with the central difference formula

\[ \frac{u_{n,1} - u_{n,-1}}{2 \Delta t} = g(x_n) \]

Rearrange for \(u_{n,-1}\)

\[ u_{n,-1} = u_{n,1} - 2 (\Delta t) g(x_n) \]

Substitute into the formula at \(k=0\)

\[ u_{n,1} = r^2 u_{n-1,0} + 2(1 - r^2) u_{n,0} + r^2 u_{n+1,0} - u_{n,1} + 2 (\Delta t) g(x_n) \]

and rearrange to get

\[ u_{n,1} = \frac{1}{2} \left( r^2 u_{n-1,0} + 2(1 - r^2) u_{n,0} + r^2 u_{n+1,0} \right) + (\Delta t) g(x_n) \]

Write as a matrix equation

\[ \boldsymbol{u}_1 = \frac{1}{2} A \boldsymbol{u}_0 + \Delta t g(\boldsymbol{x}) \]

Here we are assuming \(g(0)=g(L)=0\).

Implementation

The function waveCTCSD takes input parameters c, L, f, g, A0, AL, tf, N and K, and returns the matrix U of approximations where:

• c is the diffusion coefficient in the wavve equation \(u_{tt} = c^2 u_{xx}\)

• L is the length of the interval \(0 \leq x \leq L\)

• f is a Python function which represents the initial condition \(u(x,0) = f(x)\)

• g is a Python function which represents the initial condition \(u_t(x,0) = g(x)\)

• A0 is the boundary condition \(u(0,t) = A_0\)

• AL is the boundary condition \(u(L,t) = A_L\)

• tf is the length of the interval \(0 \leq t \leq t_f\)

• N is the number of steps in the \(x\)-direction of the discretization

• K is the number of steps in the \(t\)-direction of the discretization

• U is the matrix \(U = [u_{n,k}]\) of size \((N+1) \times (K+1)\) of approximations \(u_{n,k} \approx u(x_n,t_k)\)

def waveCTCSD(c,L,f,g,A0,AL,tf,N,K):
    dx = L/N
    dt = tf/K
    r = c*dt/dx
    x = np.linspace(0,L,N+1)
    U = np.zeros((N+1,K+1))
    U[:,0] = f(x)
    U[0,:] = A0
    U[N,:] = AL
    A = np.zeros((N+1,N+1))
    A[0,0] = 2.
    A[N,N] = 2.
    for n in range(1,N):
        A[n,n-1] = r**2
        A[n,n] = 2*(1 - r**2)
        A[n,n+1] = r**2
    G = g(x)
    G[0] = 0.
    G[N] = 0.
    U[:,1] = 1/2*A@U[:,0] + dt*G
    for k in range(1,K):
        U[:,k+1] = A@U[:,k] - U[:,k-1]
    return U

Example with Animation

Consider the equation \(u_{tt} = 0.25 u_{xx}\) for \(L=1\) with initial conditions \(u(x,0) = 1 - \cos(2 \pi x)\), \(u_t(x,0) = 0\) and dirichlet boundary conditions \(u(0,t) = u(L,t) = 0\).

c = 0.5
L = 1
f = lambda x: 1 - np.cos(2*np.pi*x)
g = lambda x: 0*x
A0 = 0
AL = 0
tf = 5
N = 50
K = 5000

U = waveCTCSD(c,L,f,g,A0,AL,tf,N,K)

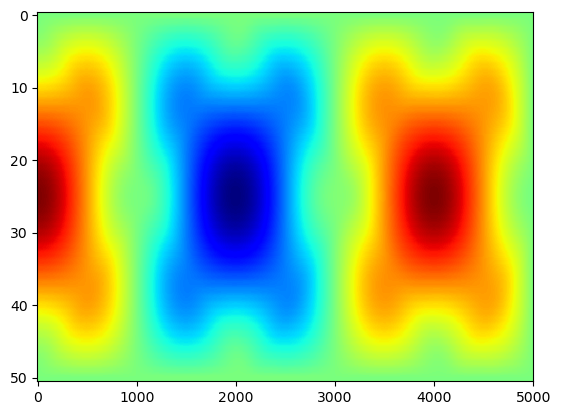
Visualize the result as a heat map:

plt.imshow(U,aspect='auto',cmap='jet')
plt.show()

Animiate the result:

nframes = 100
tstep = K//nframes
x = np.linspace(0,L,N+1)

fig,ax = plt.subplots()
line, = plt.plot([],[])
ax.set_xlim(-0.1,L+0.1)
ax.set_ylim(-2.2,2.2)
ax.grid(True)
update = lambda k: line.set_data(x,U[:,k*tstep])

ani = FuncAnimation(fig,update,frames=nframes,interval=1000*tf/nframes)
plt.close()

HTML(ani.to_html5_video())

CTCS with Neumann BCs

Matrix Equations

Consider Neumann boundary conditions \(u_x(0,t) = Q_0\) and \(u_x(L,t) = Q_L\). The CTCS finite difference equation at \(n=0\) yields

\[ u_{0,k+1} = r^2 u_{-1,k} + 2(1 - r^2) u_{0,k} + r^2 u_{1,k} - u_{0,k-1} \]

with the “ghost value” \(u_{-1,k}\). Use the central difference formula for \(u_x(0,t_k) = Q_0\)

\[ Q_0 = \frac{u_{1,k} - u_{-1,k}}{2 \Delta x} \]

Rearrange for \(u_{-1,k}\)

\[ u_{-1,k} = u_{1,k} - 2 (\Delta x) Q_0 \]

and substitute into the CTCS equation

\[ u_{0,k+1} = 2(1 - r^2) u_{0,k} + 2r^2 u_{1,k} - u_{0,k-1} - 2 r^2 (\Delta x) Q_0 \]

Similarly, the boundary condition \(u_x(L,t) = Q_L\) yields the equation

\[ u_{N,k+1} = 2r^2 u_{N-1,k} + 2(1 - r^2) u_{N,k} - u_{N,k-1} + 2 r^2 (\Delta x) Q_L \]

\[\begin{split} \begin{array}{cccccccccccccccccc} u_{0,k+1} & = & 2(1-2r^2)u_{0,k} & + & 2r^2 u_{1,k} & & & & & & & & & - & u_{0,k-1} & - & 2r^2 (\Delta x) Q_0 \\ u_{1,k+1} & = & r^2 u_{0,k} & + & 2(1 - r^2) u_{1,k} & + & r^2 u_{2,k} & & & & & & & - & u_{1,k-1} & & \\ u_{2,k+1} & = & & & r^2 u_{1,k} & + & 2(1 - r^2) u_{2,k} & + & r^2 u_{3,k} & & & & & - & u_{2,k-1} & & \\ & \vdots & & & & & & \ddots & & & & & & \vdots & & & \\ u_{N-2,k+1} & = & & & & & r^2 u_{N-3,k} & + & 2(1 - r^2) u_{N-2,k} & + & r^2 u_{N-1,k} & & & - & u_{N-2,k-1} & & \\ u_{N-1,k+1} & = & & & & & & & r^2 u_{N-2,k} & + & 2(1 - r^2) u_{N-1,k} & + & r^2 u_{N,k} & - & u_{N-1,k-1} & & \\ u_{N,k+1} & = & & & & & & & & & 2r^2 u_{N-1,k}& + & 2(1-r^2)u_{N,k} & - & u_{N,k-1} & + & 2r^2(\Delta x) Q_L \end{array} \end{split}\]

Therefore we can write the CTCS method as an iterative matrix formula

\[ \boldsymbol{u}_{k+1} = A \boldsymbol{u}_k - \boldsymbol{u}_{k-1} + \boldsymbol{q} \]

where

\[\begin{split} A = \left[ \begin{array}{ccccccc} 2(1 - r^2) & 2r^2 & & & & \\ r^2 & 2(1 - r^2) & r^2 & & & & \\ & r^2 & 2(1 - r^2) & r^2 & & & \\ & & & \ddots & & & \\ & & & r^2 & 2(1 - r^2) & r^2 & \\ & & & & r^2 & 2(1 - r^2) & r^2 \\ & & & & & 2r^2 & 2(1 - r^2) \end{array} \right] \end{split}\]

\[\begin{split} \boldsymbol{u}_k = \begin{bmatrix} u_{0,k} \\ u_{1,k} \\ \vdots \\ u_{N-1,k} \\ u_{N,k} \end{bmatrix} \hspace{20mm} \boldsymbol{q} = \begin{bmatrix} -2r^2(\Delta x) Q_0 \\ 0 \\ \vdots \\ 0 \\ 2r^2(\Delta x)Q_L \end{bmatrix} \hspace{20mm} r = \frac{c \Delta t}{\Delta x} \end{split}\]

For \(0<n<N\), the equation for \(k=0\) is just as for Dirichlet boundary conditions

\[ u_{n,1} = \frac{1}{2} \left( r^2 u_{n-1,0} + 2(1 - r^2) u_{n,0} + r^2 u_{n+1,0} \right) + (\Delta t) g(x_n) \]

For \(n=0\) we have

\[ u_{0,1} = (1 - r^2) u_{0,0} + r^2 u_{1,0} - r^2(\Delta x)Q_0 + (\Delta t) g(x_0) \]

and for \(n=N\) we have

\[ u_{N,1} = r^2 u_{N-1,0} + (1 - r^2) u_{N,0} + r^2(\Delta x)Q_L + (\Delta t) g(x_N) \]

Therefore

\[ \boldsymbol{u}_1 = \frac{1}{2} A \boldsymbol{u}_0 + \frac{1}{2}\boldsymbol{q} + \Delta t g(\boldsymbol{x}) \]

Implementation

The function waveCTCSN takes input parameters c, L, f, g, Q0, QL, tf, N and K, and returns the matrix U of approximations where:

• c is the diffusion coefficient in the wave equation \(u_{tt} = c^2 u_{xx}\)

• L is the length of the interval \(0 \leq x \leq L\)

• f is a Python function which represents the initial condition \(u(x,0) = f(x)\)

• g is a Python function which represents the initial condition \(u_t(x,0) = g(x)\)

• Q0 is the boundary condition \(u_x(0,t) = Q_0\)

• QL is the boundary condition \(u_x(L,t) = Q_L\)

• tf is the length of the interval \(0 \leq t \leq t_f\)

• N is the number of steps in the \(x\)-direction of the discretization

• K is the number of steps in the \(t\)-direction of the discretization

• U is the matrix \(U = [u_{n,k}]\) of size \((N+1) \times (K+1)\) of approximations \(u_{n,k} \approx u(x_n,t_k)\)

def waveCTCSN(c,L,f,g,A0,AL,tf,N,K):
    dx = L/N
    dt = tf/K
    r = c*dt/dx
    x = np.linspace(0,L,N+1)
    U = np.zeros((N+1,K+1))
    U[:,0] = f(x)
    A = np.zeros((N+1,N+1))
    A[0,0] = 2*(1 - r**2)
    A[0,1] = 2*r**2
    A[N,N] = 2*(1 - r**2)
    A[N,N-1] = 2*r**2
    for n in range(1,N):
        A[n,n-1] = r**2
        A[n,n] = 2*(1 - r**2)
        A[n,n+1] = r**2
    q = np.zeros(N+1)
    q[0] = -2*r**2*dx*Q0
    q[N] = 2*r**2*dx*QL
    U[:,1] = 1/2*A@U[:,0] + 1/2*q + dx*g(x)
    for k in range(1,K):
        U[:,k+1] = A@U[:,k] - U[:,k-1] + q
    return U

c = 0.5
L = 1
f = lambda x: 1 - np.cos(2*np.pi*x)
g = lambda x: 0*x
Q0 = 0
QL = 0
tf = 5
N = 50
K = 5000

U = waveCTCSN(c,L,f,g,Q0,QL,tf,N,K)

nframes = 100
tstep = K//nframes
x = np.linspace(0,L,N+1)

fig,ax = plt.subplots()
line, = plt.plot([],[])
ax.set_xlim(-0.1,L+0.1)
ax.set_ylim(-0.2,2.2)
ax.grid(True)
update = lambda k: line.set_data(x,U[:,k*tstep])

ani = FuncAnimation(fig,update,frames=nframes,interval=1000*tf/nframes)
plt.close()

HTML(ani.to_html5_video())

CTCS with Mixed BCs

Combine both functions waveCTCSD and waveCTCSN into a single function wave which takes input parameters c, L, f, g, BCtype0, BC0, BCtypeL, BCL, tf, N and K, and returns the matrix U of approximations where:

• c is the coefficient in the wave equation \(u_{tt} = c^2 u_{xx}\)

• L is the length of the interval \(0 \leq x \leq L\)

• f is a Python function which represents the initial condition \(u(x,0) = f(x)\)

• g is a Python function which represents the initial condition \(u_t(x,0) = g(x)\)

• BCtype0 is the type of boundary condition at \(x=0\) ('D' for Dirichlet or 'N' for Neumann)

• BC0 is the value of the boundary condition at \(x=0\)

• BCtypeL is the type of boundary condition at \(x=L\) ('D' for Dirichlet or 'N' for Neumann)

• BCL is the value of the boundary condition at \(x=L\)

• tf is the length of the interval \(0 \leq t \leq t_f\)

• N is the number of steps in the \(x\)-direction of the discretization

• K is the number of steps in the \(t\)-direction of the discretization

• U is the matrix \(U = [u_{n,k}]\) of size \((N+1) \times (K+1)\) of approximations \(u_{n,k} \approx u(x_n,t_k)\)

def wave(c,L,f,g,BCtype0,BC0,BCtypeL,BCL,tf,N,K):
    dx = L/N
    dt = tf/K
    r = c*dt/dx
    x = np.linspace(0,L,N+1)
    U = np.zeros((N+1,K+1))
    U[:,0] = f(x)
    A = np.zeros((N+1,N+1))
    q = np.zeros(N+1)
    G = g(x)

    if (BCtype0 not in ['D','N']) or (BCtypeL not in ['D','N']):
        raise Exception("Expecting boundary conditions of type 'D' or 'N'.")
    if BCtype0 == 'D':
        U[0,0] = BC0
        A[0,0] = 2.
        G[0] = 0.
    if BCtype0 == 'N':
        A[0,0] = 2*(1 - r**2)
        A[0,1] = 2*r**2
        q[0] = -2*r**2*dx*BC0
    if BCtypeL == 'D':
        U[N,0] = BCL
        A[N,N] = 2.
        G[N] = 0.
    if BCtypeL == 'N':
        A[N,N] = 2*(1 - r**2)
        A[N,N-1] = 2*r**2
        q[N] = 2*r**2*dx*BCL
    
    for n in range(1,N):
        A[n,n-1] = r**2
        A[n,n] = 2*(1 - r**2)
        A[n,n+1] = r**2

    U[:,1] = 1/2*A@U[:,0] + 1/2*q + dx*G
    for k in range(1,K):
        U[:,k+1] = A@U[:,k] - U[:,k-1] + q
    
    return U

c = 0.5
L = 1
f = lambda x: 1 - np.cos(2*np.pi*x)
g = lambda x: 0*x
A0 = 0
AL = 0
tf = 5
N = 50
K = 5000

U = wave(c,L,f,g,'D',A0,'D',AL,tf,N,K)

nframes = 100
tstep = K//nframes
x = np.linspace(0,L,N+1)

fig,ax = plt.subplots()
line, = plt.plot([],[])
ax.set_xlim(-0.1,L+0.1)
ax.set_ylim(-2.2,2.2)
ax.grid(True)
update = lambda k: line.set_data(x,U[:,k*tstep])

ani = FuncAnimation(fig,update,frames=nframes,interval=1000*tf/nframes)
plt.close()

HTML(ani.to_html5_video())

c = 0.5
L = 1
f = lambda x: 1 - np.cos(2*np.pi*x)
g = lambda x: 0*x
Q0 = 0
QL = 0
tf = 5
N = 50
K = 5000

U = wave(c,L,f,g,'N',Q0,'N',QL,tf,N,K)

nframes = 100
tstep = K//nframes
x = np.linspace(0,L,N+1)

fig,ax = plt.subplots()
line, = plt.plot([],[])
ax.set_xlim(-0.1,L+0.1)
ax.set_ylim(-0.2,2.2)
ax.grid(True)
update = lambda k: line.set_data(x,U[:,k*tstep])

ani = FuncAnimation(fig,update,frames=nframes,interval=1000*tf/nframes)
plt.close()

HTML(ani.to_html5_video())

c = 0.5
L = 1
f = lambda x: 1 - np.cos(2*np.pi*x)
g = lambda x: 0*x
A0 = 0
QL = 0
tf = 10
N = 50
K = 5000

U = wave(c,L,f,g,'D',A0,'N',QL,tf,N,K)

nframes = 200
tstep = K//nframes
x = np.linspace(0,L,N+1)

fig,ax = plt.subplots()
line, = plt.plot([],[])
ax.set_xlim(-0.1,L+0.1)
ax.set_ylim(-2.2,2.2)
ax.grid(True)
update = lambda k: line.set_data(x,U[:,k*tstep])

ani = FuncAnimation(fig,update,frames=nframes,interval=1000*tf/nframes)
plt.close()

HTML(ani.to_html5_video())