Complex Vectors

A complex number can be represented in the form \(z = a + i b\) and also in polar form \(z = r e^{i \theta}\). The set of vectors of length \(n\) with complex entries is a complex vector space \(\mathbb{C}^n\) with inner product \(\langle \boldsymbol{u} , \boldsymbol{v} \rangle = \boldsymbol{u}^T \overline{\boldsymbol{v}}\).

A complex number is of the form

\[ z = a + i b \]

where \(i = \sqrt{-1}\) and \(a,b \in \mathbb{R}\). The complex number \(i\) satisfies \(i^2 = -1\), the real number \(a\) is called the real part of \(z\) and \(b\) is the imaginary part, and we write \(\mathrm{Re}(z) = a\) and \(\mathrm{Im}(z) = b\). The polar form of a complex number \(z = a + i b\) is

\[ z = r e^{i \theta} \]

where \(r = \sqrt{a^2 + b^2}\) and \(\theta = \arctan(b/a)\). We visualize the set of complex numbers \(\mathbb{C}\) as a 2-dimensional real vector space:

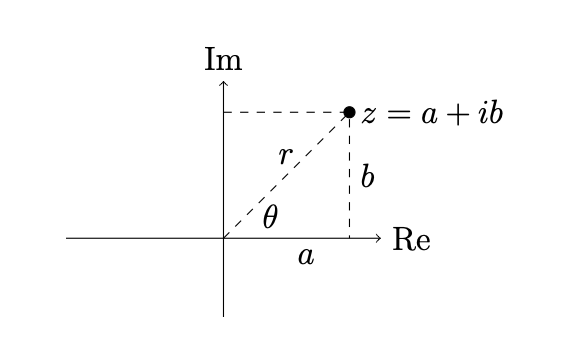
Euler’s formula is

\[ e^{i \theta} = \cos \theta + i \sin \theta \]

Let \(z = a + ib\) and \(z = re^{i \theta}\) in polar form.

1. The modulus of \(z\) is \(|z| = r = \sqrt{a^2 + b^2}\).

2. The angle (or argument) of \(z\) is \(\angle z = \theta = \arctan(b/a)\) (or \(\mathrm{arg}(z) = \theta\)).

3. The conjugate of \(z\) is \(\overline{z} = a - ib = re^{- i \theta}\).

The inverse of \(z \in \mathbb{C}\) is given by

\[ z^{-1} = \frac{\overline{z} \ \, }{|z|^2} \]

---

Proof. Let \(z = a + ib\). Then

\[ z^{-1} = \frac{1}{z} = \frac{\overline{z}}{z \overline{z}} \]

and we see

\[ z \overline{z} = (a + ib)(a - ib) = a^2 + b^2 = |z|^2 \]

The complex vector space \(\mathbb{C}^n\) is the set of vectors of length \(n\)

\[\begin{split} \boldsymbol{v} = \begin{bmatrix} v_1 \\ \vdots \\ v_n \end{bmatrix} \end{split}\]

with complex entries \(v_1, \dots, v_n \in \mathbb{C}\). The conjugate of a vector \(\boldsymbol{v} \in \mathbb{C}^n\) is given by the conjugate of each entry

\[\begin{split} \overline{\boldsymbol{v}} = \begin{bmatrix} \overline{v}_1 \\ \vdots \\ \overline{v}_n \end{bmatrix} \end{split}\]

The standard inner product of vectors \(\boldsymbol{u},\boldsymbol{v} \in \mathbb{C}^n\) is

\[ \langle \boldsymbol{u} , \boldsymbol{v} \rangle = \boldsymbol{u}^T \overline{ \boldsymbol{v} } = u_1 \overline{v}_1 + \cdots + u_n \overline{v}_n \]

Let \(\boldsymbol{u} , \boldsymbol{v} \in \mathbb{C}^n\) and let \(c \in \mathbb{C}\).

1. \(\langle c \, \boldsymbol{u} , \boldsymbol{v} \rangle = c \, \langle \boldsymbol{u} , \boldsymbol{v} \rangle\)

2. \(\langle \boldsymbol{u} , c \, \boldsymbol{v} \rangle = \overline{c} \, \langle \boldsymbol{u} , \boldsymbol{v} \rangle\)

3. \(\langle \boldsymbol{u} , \boldsymbol{v} \rangle = \overline{\langle \boldsymbol{v} , \boldsymbol{u} \rangle}\)

4. \(\langle \boldsymbol{v} , \boldsymbol{v} \rangle \geq 0\) for all \(\boldsymbol{v}\), and \(\langle \boldsymbol{v} , \boldsymbol{v} \rangle = 0\) if and only if \(\boldsymbol{v} = \boldsymbol{0}\) is the zero vector.

The norm \(\boldsymbol{v} \in \mathbb{C}^n\) is

\[ \| \boldsymbol{v} \| = \sqrt{ \langle \boldsymbol{v} , \boldsymbol{v} \rangle } = \sqrt{ |v_1|^2 + \cdots + |v_n|^2 } \]

Complex vectors \(\boldsymbol{u} , \boldsymbol{v} \in \mathbb{C}^n\) are orthogonal if \( \langle \boldsymbol{u} , \boldsymbol{v} \rangle = 0\).

The conjugate transpose of a complex matrix \(A\) is \(A^* = \overline{A}^T\). Note that \(\langle A \boldsymbol{u} , \boldsymbol{v} \rangle = \langle \boldsymbol{u} , A^* \boldsymbol{v} \rangle\)

A complex matrix \(A\) is hermitian if \(A = A*\).

If \(A\) is hermitian then \(\langle A \boldsymbol{u} , \boldsymbol{v} \rangle = \langle \boldsymbol{u} , A \boldsymbol{v} \rangle\) for all \(\boldsymbol{u} , \boldsymbol{v} \in \mathbb{C}^n\).

A complex matrix \(A\) is unitary if \(A^{-1} = A^*\).

If \(A\) is unitary then \(\langle A \boldsymbol{u} , A \boldsymbol{v} \rangle = \langle \boldsymbol{u} , \boldsymbol{v} \rangle\) for all \(\boldsymbol{u} , \boldsymbol{v} \in \mathbb{C}^n\).