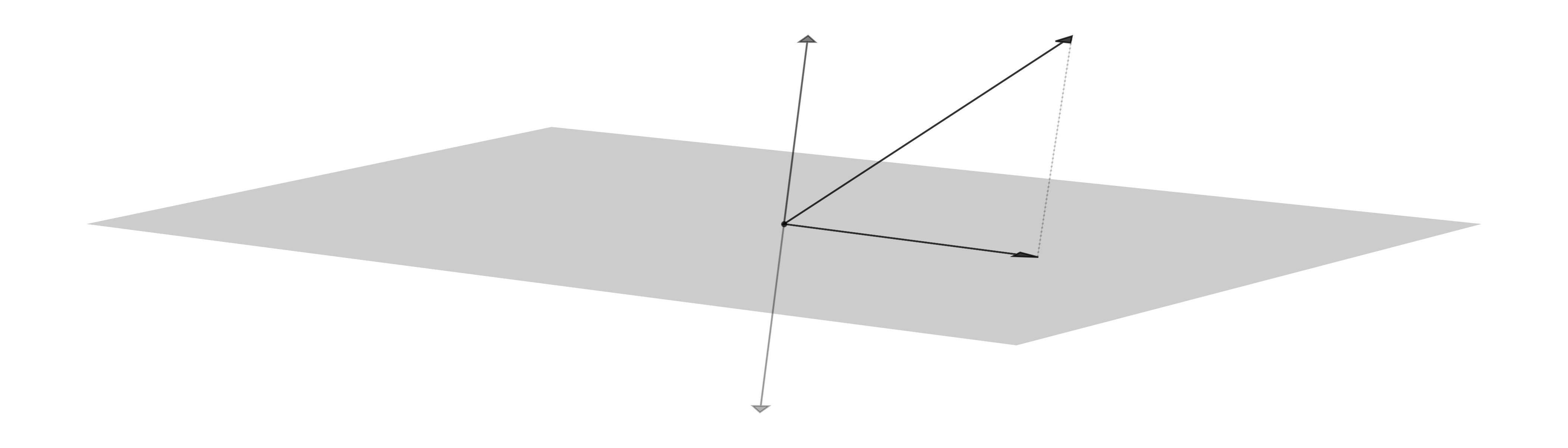
Orthogonal Bases
Let \(U \subseteq \mathbb{R}^n\) be a subspace. A set of vectors \(\{ \boldsymbol{w}_1,\dots,\boldsymbol{w}_m \}\) is an orthogonal basis for \(U\) if it is a basis for \(U\) and the vectors are orthogonal, \(\langle \boldsymbol{w}_i , \boldsymbol{w}_j \rangle = 0\) for all \(i \not= j\). Furthermore, if each \(\boldsymbol{w}_j\) is a unit vector, \(\|\boldsymbol{w}_j\| = 1\), then \(\{ \boldsymbol{w}_1,\dots,\boldsymbol{w}_m \}\) is an orthonormal basis for \(U\).
Let \(\{ \boldsymbol{u}_1 , \dots , \boldsymbol{u}_m \}\) be a basis of a subspace \(U \subseteq \mathbb{R}^n\). The Gram-Schmidt orthogonalization algorithm constructs an orthogonal basis of \(U\):
\[\begin{split}
\begin{align*}
\boldsymbol{v}_1 &= \boldsymbol{u}_1 \\
\boldsymbol{v}_2 &= \boldsymbol{u}_2 - \mathrm{proj}_{\boldsymbol{v}_1}(\boldsymbol{u}_2) \\
\boldsymbol{v}_3 &= \boldsymbol{u}_3 - \mathrm{proj}_{\boldsymbol{v}_1}(\boldsymbol{u}_3) - \mathrm{proj}_{\boldsymbol{v}_2}(\boldsymbol{u}_3) \\
& \ \ \vdots \\
\boldsymbol{v}_m &= \boldsymbol{u}_m - \mathrm{proj}_{\boldsymbol{v}_1}(\boldsymbol{u}_m) - \mathrm{proj}_{\boldsymbol{v}_2}(\boldsymbol{u}_m) - \cdots - \mathrm{proj}_{\boldsymbol{v}_{m-1}}(\boldsymbol{u}_m)
\end{align*}
\end{split}\]
Then \(\{ \boldsymbol{v}_1 , \dots , \boldsymbol{v}_m \}\) is an orthogonal basis of \(U\). Furthermore, let
\[
\boldsymbol{w}_k = \frac{\boldsymbol{v}_k}{\| \boldsymbol{v}_k \|} \ \ , \ k=1,\dots,m
\]
Then \(\{ \boldsymbol{w}_1 , \dots , \boldsymbol{w}_m \}\) is an orthonormal basis of \(U\).
Construct an orthonormal basis of the subspace \(U\) spanned by
\[\begin{split}
\boldsymbol{u}_1 = \begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \end{bmatrix}
\hspace{5mm}
\boldsymbol{u}_2 = \begin{bmatrix} 1 \\ 1 \\ 1 \\ 0 \end{bmatrix}
\hspace{5mm}
\boldsymbol{u}_3 = \begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix}
\end{split}\]
Compute
\[\begin{split}
\begin{align*}
\boldsymbol{v}_1 &= \boldsymbol{u}_1 \\
\boldsymbol{v}_2 &= \boldsymbol{u}_2 - \mathrm{proj}_{\boldsymbol{v}_1}(\boldsymbol{u}_2) \\
\boldsymbol{v}_3 &= \boldsymbol{u}_3 - \mathrm{proj}_{\boldsymbol{v}_1}(\boldsymbol{u}_3) - \mathrm{proj}_{\boldsymbol{v}_2}(\boldsymbol{u}_3)
\end{align*}
\end{split}\]
and we find an orthogonal basis
\[\begin{split}
\boldsymbol{v}_1 = \begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \end{bmatrix}
\hspace{5mm}
\boldsymbol{v}_2 = \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}
\hspace{5mm}
\boldsymbol{v}_3 = \frac{1}{2} \left[ \begin{array}{r} 1 \\ 0 \\ -1 \\ 0 \end{array} \right]
\end{split}\]
and an orthonormal basis
\[\begin{split}
\boldsymbol{w}_1 = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \end{bmatrix}
\hspace{5mm}
\boldsymbol{w}_2 = \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}
\hspace{5mm}
\boldsymbol{w}_3 = \frac{1}{\sqrt{2}} \left[ \begin{array}{r} 1 \\ 0 \\ -1 \\ 0 \end{array} \right]
\end{split}\]
Projection onto a Subpsace
Let \(U \subseteq \mathbb{R}^n\) be a subspace and let \(\{ \boldsymbol{u}_1, \dots, \boldsymbol{u}_m \}\) be an orthogonal basis of \(U\). The projection of a vector \(\boldsymbol{x}\) onto \(U\) is
\[
\mathrm{proj}_U(\boldsymbol{x}) = \frac{\langle \boldsymbol{x} , \boldsymbol{u}_1 \rangle}{ \langle \boldsymbol{u}_1 , \boldsymbol{u}_1 \rangle } \boldsymbol{u}_1 + \cdots + \frac{\langle \boldsymbol{x} , \boldsymbol{u}_m \rangle}{ \langle \boldsymbol{u}_m , \boldsymbol{u}_m \rangle } \boldsymbol{u}_m
\]
Projection onto \(U\) is given by matrix multiplication
\[
\mathrm{proj}_{\boldsymbol{U}}(\boldsymbol{x}) = P \boldsymbol{x}
\ \ \text{where} \ \
P = \frac{1}{\| \boldsymbol{u}_1 \|^2} \boldsymbol{u}_1 \boldsymbol{u}_1^T + \cdots + \frac{1}{\| \boldsymbol{u}_m \|^2} \boldsymbol{u}_m \boldsymbol{u}_m^T
\]
Note that \(P^2 = P\), \(P^T = P\) and \(\mathrm{rank}(P) = m\).
A matrix \(P\) is an orthogonal projector (or orthogonal projection matrix) if \(P^2 = P\) and \(P^T = P\).
Let \(P\) be the orthogonal projection onto \(U\). Then \(I - P\) is the orthogonal projection matrix onto \(U^{\perp}\).
Find the orthogonal projection matrix \(P\) which projects onto the subspace spanned by the vectors
\[\begin{split}
\boldsymbol{u}_1 = \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right]
\hspace{5mm}
\boldsymbol{u}_2 = \left[ \begin{array}{r} 1 \\ 1 \\ 1 \end{array} \right]
\end{split}\]
Compute \(\langle \boldsymbol{u}_1 , \boldsymbol{u}_2 \rangle = 0\) therefore the vectors are orthogonal. Compute
\[\begin{split}
\begin{align*}
P &= \frac{1}{\| \boldsymbol{u}_1 \|^2} \boldsymbol{u}_1 \boldsymbol{u}_1^T + \frac{1}{\| \boldsymbol{u}_2 \|^2} \boldsymbol{u}_2 \boldsymbol{u}_2^T \\
&= \frac{1}{2} \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right]
\left[ \begin{array}{rrr} 1 & 0 & -1 \end{array} \right]
+ \frac{1}{3} \left[ \begin{array}{r} 1 \\ 1 \\ 1 \end{array} \right]
\left[ \begin{array}{rrr} 1 & 1 & 1 \end{array} \right] \\
&= \frac{1}{2} \left[ \begin{array}{rrr} 1 & \phantom{+}0 & -1 \\ 0 & 0 & 0 \\ -1 & 0 & 1 \end{array} \right]
+ \frac{1}{3} \left[ \begin{array}{rrr} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array} \right]
=
\frac{1}{6} \left[ \begin{array}{rrr} 5 & \phantom{+}2 & -1 \\ 2 & 2 & 2 \\ -1 & 2 & 5 \end{array} \right]
\end{align*}
\end{split}\]
Find the orthogonal projection matrix \(P_{\perp}\) which projects onto \(U^{\perp}\) where \(U\) the subspace spanned by the vectors
\[\begin{split}
\boldsymbol{u}_1 = \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right]
\hspace{5mm}
\boldsymbol{u}_2 = \left[ \begin{array}{r} 1 \\ 1 \\ 1 \end{array} \right]
\end{split}\]
as in the previous example. Compute
\[\begin{split}
\begin{align*}
P_{\perp} = I - P &=
\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] -
\frac{1}{6} \left[ \begin{array}{rrr} 5 & \phantom{+}2 & -1 \\ 2 & 2 & 2 \\ -1 & 2 & 5 \end{array} \right] \\
&= \frac{1}{6} \left[ \begin{array}{rrr} 1 & -2 & 1 \\ -2 & 4 & -2 \\ 1 & -2 & 1 \end{array} \right]
\end{align*}
\end{split}\]
Note that
\[\begin{split}
\boldsymbol{u}_3 = \left[ \begin{array}{r} 1 \\ -2 \\ 1 \end{array} \right]
\end{split}\]
is orthogonal to both \(\boldsymbol{u}_1\) and \(\boldsymbol{u}_2\) and is a basis of the orthogonal complement \(U^{\perp}\). Therefore we could also compute
\[\begin{split}
\begin{align*}
P_{\perp} = \frac{1}{\| \boldsymbol{u}_3 \|^2} \boldsymbol{u}_3 \boldsymbol{u}_3^T
&= \frac{1}{6} \left[ \begin{array}{r} 1 \\ -2 \\ 1 \end{array} \right]
\left[ \begin{array}{ccc} 1 & -2 & 1 \end{array} \right] \\
&= \frac{1}{6} \left[ \begin{array}{rrr} 1 & -2 & 1 \\ -2 & 4 & -2 \\ 1 & -2 & 1 \end{array} \right]
\end{align*}
\end{split}\]
Exercises
Let \(\boldsymbol{u}\) and \(\boldsymbol{v}\) be nonzero column vectors in \(\mathbb{R}^n\) such that \(\langle \boldsymbol{u} , \boldsymbol{v} \rangle = 0\) and let
\[
P = \frac{1}{\| \boldsymbol{u} \| \| \boldsymbol{v} \|} \boldsymbol{v} \boldsymbol{u}^T
\]
Determine whether the statement is True or False.
\(\mathrm{rank}(P) = 1\)
\(P^2\) is the identity matrix
\(P^2\) is the zero matrix
\(P \boldsymbol{x}\) is the projection \(\boldsymbol{x}\) onto \(\boldsymbol{u}\)
\(P \boldsymbol{x}\) is the projection \(\boldsymbol{x}\) onto \(\boldsymbol{v}\)
\(P \boldsymbol{u} = c \boldsymbol{v}\) for some nonzero number \(c\)
True
False
True
False
False
True
Let \(U \subset \mathbb{R}^n\) be a subspace. Let \(P_1\) be the orthogonal projector onto \(U\) and let \(P_2\) be the orthogonal projector onto the orthogonal complement \(U^{\perp}\). Determine whether the statement is True or False.
\(I = P_1 + P_2\)
\(P_1P_2 = P_2P_1 = 0\)
Let \(U \subset \mathbb{R}^3\) be the subspace spanned by
\[\begin{split}
\boldsymbol{u}_1 = \left[ \begin{array}{r} 1 \\ 1 \\ 1 \end{array} \right]
\hspace{10mm}
\boldsymbol{u}_2 = \left[ \begin{array}{r} -1 \\ 1 \\ 1 \end{array} \right]
\end{split}\]
Find the vector in \(U\) which is closest to the vector
\[\begin{split}
\boldsymbol{x} = \left[ \begin{array}{r} 1 \\ 2 \\ 1 \end{array} \right]
\end{split}\]
\[\begin{split}
\mathrm{proj}_U(\boldsymbol{x}) = \begin{bmatrix} 1 \\ 3/2 \\ 3/2 \end{bmatrix}
\end{split}\]
Let \(U \subset \mathbb{R}^3\) be the subspace spanned by
\[\begin{split}
\boldsymbol{u}_1 = \left[ \begin{array}{r} 1 \\ 1 \\ 1 \end{array} \right]
\hspace{10mm}
\boldsymbol{u}_2 = \left[ \begin{array}{r} 1 \\ 2 \\ 1 \end{array} \right]
\end{split}\]
Find the shortest distance from \(\boldsymbol{x}\) to \(U\) where
\[\begin{split}
\boldsymbol{x} = \left[ \begin{array}{r} 1 \\ 1 \\ 2 \end{array} \right]
\end{split}\]
\[
\| \boldsymbol{x} - \mathrm{proj}_U(\boldsymbol{x}) \| = \frac{1}{\sqrt{2}}
\]
Let \(\boldsymbol{u} \in \mathbb{R}^n\) be a nonzero vector and let
\[
H = I - \frac{2}{\| \boldsymbol{u} \|^2}\boldsymbol{u} \boldsymbol{u}^T
\]
The matrix \(H\) is called an elementary reflector. Determine whether the statement is True or False.
There is a unique unit vector \(\boldsymbol{v}\) such that \(H \boldsymbol{v} = \boldsymbol{v}\).
\(H \boldsymbol{v} = \boldsymbol{v}\) for all \(\boldsymbol{v} \in \mathrm{span} \{ \boldsymbol{u} \}^{\perp}\).