Diagonalization

An \(n \times n\) matrix \(A\) is diagonalizable if and only if \(A\) has \(n\) linearly independent eigenvectors. If a matrix \(A\) is real and symmetric then it is diagonalizable, the eigenvalues are real numbers and the eigenvectors (for distinct eigenvalues) are orthogonal.

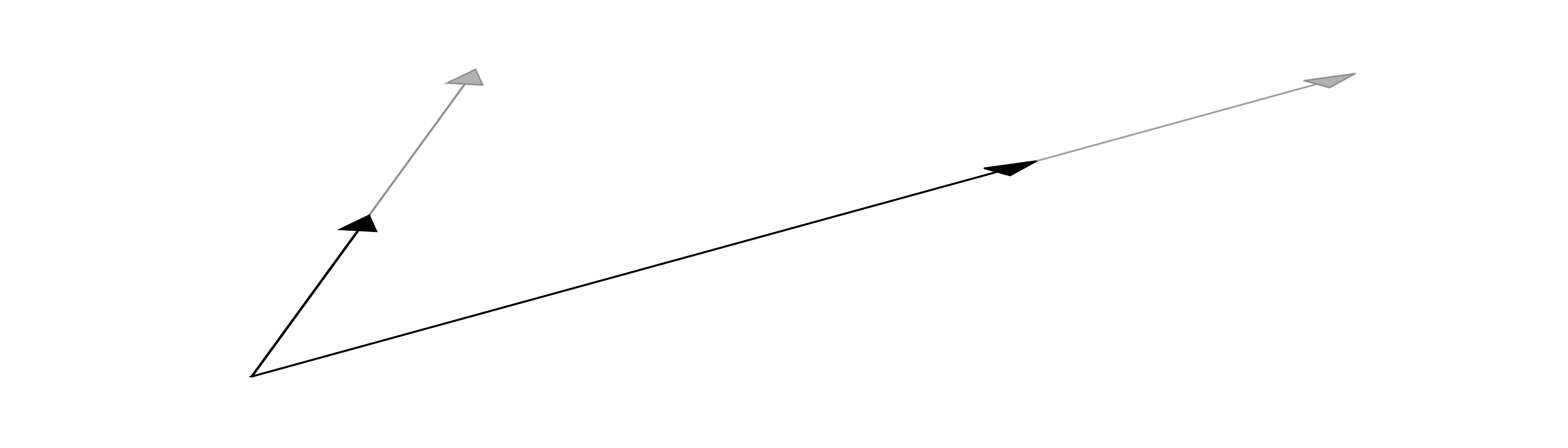
Eigenvalues and Eigenvectors

An eigenvalue of a matrix \(A\) is a number \(\lambda\) such that

\[ A \boldsymbol{v} = \lambda \boldsymbol{v} \]

for some nonzero vector \(\boldsymbol{v}\). The vector \(\boldsymbol{v}\) is called an eigenvector for the eigenvalue \(\lambda\). Eigenvalues of a real matrix may be real or complex numbers.

If \(\lambda\) is an eigenvalue of \(A\) with eigenvector \(\boldsymbol{v}\) then \((A - \lambda I)\boldsymbol{v} = \boldsymbol{0}\) which implies that \(A - \lambda I\) is not invertible and therefore \(\det(A - \lambda I) = 0\). This suggests that to find eigenvalues and eigenvectors of \(A\) we should:

1. Find \(\lambda\) such that \(\det(A - \lambda I) = 0\).

2. Find solutions of the linear system \((A - \lambda I)\boldsymbol{v} = \boldsymbol{0}\).

This works when \(A\) is a small matrix and we have done this in previous linear algebra courses. However, this is impractical when \(A\) is a large matrix. For example, if \(A\) is \(5 \times 5\), then \(\det(A - \lambda I) = 0\) is a polynomial equation of degree 5 and there is no formula for the roots. We’ll see better algorithms for computing eigenvalues in later sections.

Let \(A\) be an \(n \times n\) matrix. The characteristic polynomial of \(A\) is

\[ c_A(x) = \det(A - xI) \]

where \(I\) is the identity matrix. The polynomial \(c_A(x)\) has degree \(n\) and the roots of \(c_A(x)\) are the eigenvalues of \(A\).

Diagonalization

A matrix \(A\) is diagonalizable if there exists an invertible matrix \(P\) and a diagonal matrix \(D\) such that \(A = PD P^{-1}\).

If \(A\) is diagonalizable with \(A = PDP^{-1}\) then the diagonal entries of \(D\) are eigenvalues of \(A\) and the columns of \(P\) are the corresponding eigenvectors.

Proof

Let \(\boldsymbol{v}_1,\dots, \boldsymbol{v}_n\) be the columns of \(P\) and let \(\lambda_1,\dots,\lambda_n\) be the diagonal entries of \(D\)

\[\begin{split} P = \begin{bmatrix} & & \\ \boldsymbol{v}_1 & \cdots & \boldsymbol{v}_n \\ & & \end{bmatrix} \hspace{10mm} D = \begin{bmatrix} \lambda_1 & & \\ & \ddots & \\ & & \lambda_n \end{bmatrix} \end{split}\]

Matrix multiplication \(AP = PD\) yields the equation

\[\begin{split} \begin{align*} A \begin{bmatrix} & & \\ \boldsymbol{v}_1 & \cdots & \boldsymbol{v}_n \\ & & \end{bmatrix} &= \begin{bmatrix} & & \\ \boldsymbol{v}_1 & \cdots & \boldsymbol{v}_n \\ & & \end{bmatrix} \begin{bmatrix} \lambda_1 & & \\ & \ddots & \\ & & \lambda_n \end{bmatrix} \\ \begin{bmatrix} & & \\ A \boldsymbol{v}_1 & \cdots & A \boldsymbol{v}_n \\ & & \end{bmatrix} &= \begin{bmatrix} & & \\ \lambda_1 \boldsymbol{v}_1 & \cdots & \lambda_n \boldsymbol{v}_n \\ & & \end{bmatrix} \end{align*} \end{split}\]

Therefore \(A \boldsymbol{v}_i = \lambda_i \boldsymbol{v}_i\) for each \(i=1,\dots,n\).

If \(A\) has distinct eigenvalues then \(A\) is diagonalizable.

Proof

Let \(\lambda_1,\dots,\lambda_n\) be the distinct eigenvalues of \(A\). That is, \(\lambda_i \not= \lambda_j\) for \(i \ne j\). Each \(\lambda_i\) has a corresponding eigenvector \(\boldsymbol{v}_i\). Construct \(P\) with eigenvectors in the columns

\[\begin{split} P = \begin{bmatrix} & & \\ \boldsymbol{v}_1 & \cdots & \boldsymbol{v}_n \\ & & \end{bmatrix} \end{split}\]

and construct \(D\) with the eigenvalues in the diagonal entries

\[\begin{split} D = \begin{bmatrix} \lambda_1 & & \\ & \ddots & \\ & & \lambda_n \end{bmatrix} \end{split}\]

Then \(A = PDP^{-1}\) by construction.

By the Fundamental Theorem of Algebra, the characteristic polynomial of a matrix \(A\) factors as a product

\[ c_A(x) = \pm \prod_{i=1}^k (x - \lambda_i)^{m_i} \]

where \(\lambda_1, \dots, \lambda_k\) are the distinct eigenvalues of \(A\). The algebraic multiplicity of \(\lambda_i\) is the power \(m_i\) in the factored characteristic polynomial. In other words, the algebraic multiplicity of \(\lambda_i\) is the number of times \(\lambda_i\) occurs as a root of the characteristic polynomial \(c_A(x)\).

Let \(\lambda\) be an eigenvalue of \(A\). The geometric multiplicity of \(\lambda\) is the number of linearly independent eigenvectors corresponding to \(\lambda\). In other words, the geometric multiplicity is the dimension of the eigenspace for \(\lambda\)

\[ E_{\lambda} = N(A - \lambda I) = \{ \boldsymbol{v} \in \mathbb{R}^n : (A - \lambda I) \boldsymbol{v} = \boldsymbol{0} \} \]

Not every matrix is diagonalizable. For example, consider the matrix

\[\begin{split} A = \begin{bmatrix} 3 & 1 \\ 0 & 3 \end{bmatrix} \end{split}\]

Then \(c_A(x) = (x - 3)^2\) and there is only one eigenvalue \(\lambda = 3\) and it has algebraic multiplicity 2. Solving the equation \((A - 3I)\boldsymbol{v} = \boldsymbol{0}\) yields only one independent solution

\[\begin{split} \boldsymbol{v} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \end{split}\]

and so \(\lambda = 3\) has geometric multiplicity 1. Therefore \(A\) does not have enough eigenvectors to be diagonalizable.

A matrix \(A\) is diagonalizable if and only if, for all eiganvalues \(\lambda\), the algebraic multiplicity of \(\lambda\) equals the geometric multiplicity of \(\lambda\).

Spectral Theorem

All eigenvalues of a symmetric matrix are real numbers.

Proof

Let \(\lambda\) be an eigenvalue of a symmetric matrix \(A\) with eigenvector \(\boldsymbol{v}\). Compute the complex inner product \(\langle \boldsymbol{v} , A \boldsymbol{v} \rangle = \boldsymbol{v}^T \, \overline{A \boldsymbol{v}}\) in two different ways. First, compute

\[ \langle \boldsymbol{v} , A \boldsymbol{v} \rangle = \langle \boldsymbol{v} , \lambda \boldsymbol{v} \rangle = \overline{\lambda} \langle \boldsymbol{v} , \boldsymbol{v} \rangle = \overline{\lambda} \, \| \boldsymbol{v} \|^2 \]

Since \(A\) is real and symmetric, we have \(\overline{A}^T = A\) and we compute

\[ \langle \boldsymbol{v} , A \boldsymbol{v} \rangle = \langle \overline{A}^T \boldsymbol{v} , \boldsymbol{v} \rangle = \langle A \boldsymbol{v} , \boldsymbol{v} \rangle = \lambda \langle \boldsymbol{v} , \boldsymbol{v} \rangle = \lambda \| \boldsymbol{v} \|^2 \]

Since \(\| \boldsymbol{v} \| \not= 0\) we have \(\lambda = \overline{\lambda}\) and therefore \(\lambda\) is a real number.

Let \(A\) be a symmetric matrix and let \(\lambda_1\) and \(\lambda_2\) be distinct real eigenvalues of \(A\) with eigenvectors \(\boldsymbol{v}_1\) and \(\boldsymbol{v}_2\) respectively. Then \(\boldsymbol{v}_1\) and \(\boldsymbol{v}_2\) are orthogonal.

Proof

Since \(\lambda_1\) and \(\lambda_2\) are real eigenvalues we may assume \(\boldsymbol{v}_1\) and \(\boldsymbol{v}_2\) are real vectors. Compute \(\langle A \boldsymbol{v}_1 , \boldsymbol{v}_2 \rangle\) in two different ways. First, compute

\[ \langle A \boldsymbol{v}_1 , \boldsymbol{v}_2 \rangle = \langle \lambda_1 \boldsymbol{v}_1 , \boldsymbol{v}_2 \rangle = \lambda_1 \langle \boldsymbol{v}_1 , \boldsymbol{v}_2 \rangle \]

Now compute

\[ \langle A \boldsymbol{v}_1 , \boldsymbol{v}_2 \rangle = \langle \boldsymbol{v}_1 , A^T \boldsymbol{v}_2 \rangle = \langle \boldsymbol{v}_1 , A \boldsymbol{v}_2 \rangle = \lambda_2 \langle \boldsymbol{v}_1 , \boldsymbol{v}_2 \rangle \]

Therefore

\[ \lambda_1 \langle \boldsymbol{v}_1 , \boldsymbol{v}_2 \rangle = \lambda_2 \langle \boldsymbol{v}_1 , \boldsymbol{v}_2 \rangle \ \ \Rightarrow \ \ (\lambda_1 - \lambda_2) \langle \boldsymbol{v}_1 , \boldsymbol{v}_2 \rangle = 0 \ \ \Rightarrow \ \ \langle \boldsymbol{v}_1 , \boldsymbol{v}_2 \rangle = 0 \]

since \(\lambda_1 - \lambda_2 \not = 0\) because the eigenvalues are distinct.

Let \(A\) be a symmetric matrix. Then there exists an orthogonal matrix \(P\) and diagonal matrix \(D\) such that \(A = PDP^T\). In other words, \(A\) is orthogonally diagonalizable.

Exercises

Determine whether the statement is True or False.

• Let \(\boldsymbol{v}_1 , \boldsymbol{v}_2 \in \mathbb{R}^2\) be linearly independent vectors. Let \(\lambda_1 , \lambda_2\) be real numbers. There exists a unique \(2 \times 2\) matrix \(A\) with eigenvalues \(\lambda_1 , \lambda_2\) and corresponding eigenvectors \(\boldsymbol{v}_1 , \boldsymbol{v}_2\).

• Suppose \(A\) and \(B\) are symmetric \(n \times n\) matrices. The eigenvectors of \(AB\) corresponding to distinct eigenvalues are orthogonal.

Solution

• True

• False

Let \(A\) be a \(m \times n\) matrix. Determine whether the statement is True or False.

• If \(\lambda\) is an eigenvalue of \(AA^T\) then \(\lambda\) is a real number.

• If \(\boldsymbol{v}_1 , \boldsymbol{v}_2\) are eigenvectors of \(AA^T\) for distinct eigenvalues \(\lambda_1 , \lambda_2\) then \(\langle \boldsymbol{v}_1 , \boldsymbol{v}_1 \rangle = 0\).

Solution

• True

• True

Let \(U \subset \mathbb{R}^n\) be a subspace with \(\mathrm{dim}(U) = m\) such that \(0 < m < n\), and let \(P\) be the orthogonal projection matrix onto \(U\). Determine the characteristic polynomial of \(P\).

Solution

\[ c_P(x) = \pm (x-1)^m x^{n-m} \]

Let \(\boldsymbol{u} \in \mathbb{R}^n\) be a nonzero vector and let

\[ H = I - \frac{2}{\| \boldsymbol{u} \|^2} \boldsymbol{u} \boldsymbol{u}^T \]

be the corresponding elementary reflector. Determine the characteristic polynomial of \(H\).

Solution

\[ c_H(x) = \pm (x-1)^{n-1} (x+1) \]

Let \(\lambda\) be a eigenvalue of an invertible matrix \(A\). Determine whether the statement is True or False.

• \(\lambda^{-1}\) is an eigenvalue of \(A^{-1}\)

• \(\lambda\) is an eigenvalue of \(A^T\)

• \(\lambda^2\) is an eigenvalue of \(AA^T\)

• \(\lambda\) is an eigenvalue of \(BAB^{-1}\) for any invertible matrix \(B\)

• \(\lambda \ne 0\)

Solution

• True

• True

• False

• True

• True

Suppose \( A \) is a symmetric \( 3 \times 3 \) matrix with distinct eigenvalues \( \lambda_1 , \lambda_2 , \lambda_3 \) and eigenvectors

\[\begin{split} \boldsymbol{v}_1 = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} \hspace{10mm} \boldsymbol{v}_2 = \begin{bmatrix} 1 \\ 0 \\ -1 \end{bmatrix} \end{split}\]

Find an eigenvector \(\boldsymbol{v}_3\) for eigenvalue \(\lambda_3\).

Solution

\[\begin{split} \boldsymbol{v}_3 = \left[ \begin{array}{r} 1 \\ -2 \\ 1 \end{array} \right] \end{split}\]