Orthogonal Complement#

The orthogonal complement \(U^{\perp}\) of a subspace \(U\) is the collection of all vectors which are orthogonal to every vector in \(U\).

../_images/02_02_01.png

Orthogonal Vectors#

The inner product of vectors \(\boldsymbol{x}, \boldsymbol{y} \in \mathbb{R}^n\) is

\[ \langle \boldsymbol{x} , \boldsymbol{y} \rangle = \sum_{k=1}^n x_k y_k = x_1y_1 + \cdots + x_ny_n \]

Let’s summarize various properties of the inner product:

The inner product is symmetric: \(\langle \boldsymbol{x} , \boldsymbol{y} \rangle = \langle \boldsymbol{y} , \boldsymbol{x} \rangle\) for all \(\boldsymbol{x}, \boldsymbol{y} \in \mathbb{R}^n\).

The inner product of column vectors is the same as matrix multiplication:

\[\begin{split} \langle \boldsymbol{x} , \boldsymbol{y} \rangle = \boldsymbol{x}^T \boldsymbol{y} = \begin{bmatrix} x_1 & \cdots & x_n \end{bmatrix} \begin{bmatrix} y_1 \\ \vdots \\ y_n \end{bmatrix} \end{split}\]

The inner product satisfies the usual distributive rules of multiplication:

\[ \langle \boldsymbol{x} , c \boldsymbol{y} + d \boldsymbol{z} \rangle = c \langle \boldsymbol{x} , \boldsymbol{y} \rangle + d \langle \boldsymbol{x} , \boldsymbol{z} \rangle \]

for all \(c,d \in \mathbb{R}\) and \(\boldsymbol{x} , \boldsymbol{y} , \boldsymbol{z} \in \mathbb{R}^n\).

The square root of the inner product of a vector \(\boldsymbol{x}\) with itself is equal to the 2-norm

\[ \sqrt{ \langle \boldsymbol{x} , \boldsymbol{x} \rangle } = \| \boldsymbol{x} \| \]

We can also write the inner product in terms of the angle between vectors

\[ \langle \boldsymbol{x} , \boldsymbol{y} \rangle = \| \boldsymbol{x} \| \| \boldsymbol{y} \| \cos \theta \hspace{10mm} 0 \leq \theta \leq \pi \]

Let \(A\) be a \(m \times n\) matrix, let \(\boldsymbol{u} \in \mathbb{R}^n\) and let \(\boldsymbol{v} \in \mathbb{R}^m\). Then

\[ \langle A \boldsymbol{u} , \boldsymbol{v} \rangle = \langle \boldsymbol{u} , A^T \boldsymbol{v} \rangle \]

Vectors \(\boldsymbol{x}, \boldsymbol{y} \in \mathbb{R}^n\) are orthogonal if \(\langle \boldsymbol{x} , \boldsymbol{y} \rangle = 0\). More generally, vectors \(\boldsymbol{x}_1, \dots, \boldsymbol{x}_m \in \mathbb{R}^n\) are orthogonal if \(\langle \boldsymbol{x}_i , \boldsymbol{x}_j \rangle = 0\) for all \(i \not= j\). In other words, each \(\boldsymbol{x}_i\) is orthogonal to every other vector \(\boldsymbol{x}_j\) in the set. Furthermore, vectors \(\boldsymbol{x}_1, \dots, \boldsymbol{x}_m \in \mathbb{R}^n\) are orthonormal if they are orthogonal and each is a unit vector, \(\| \boldsymbol{x}_k \| = 1\), \(k=1,\dots,m\).

Vectors \(\boldsymbol{x}, \boldsymbol{y} \in \mathbb{R}^n\) are orthogonal if and only if the acute angle between \(\boldsymbol{x}\) and \(\boldsymbol{y}\) is \(\pi/2\) radians (or 90 degrees).

Let \(\boldsymbol{x}_1, \dots, \boldsymbol{x}_m \in \mathbb{R}^n\) be orthogonal. Then

\[ \| \boldsymbol{x}_1 + \cdots + \boldsymbol{x}_m \|^2 = \| \boldsymbol{x}_1 \|^2 + \cdots + \| \boldsymbol{x}_m \|^2 \]

This is called the Pythagorean theorem.

Proof. Compute the left side of the equation using orthogonality \(\langle \boldsymbol{x}_i , \boldsymbol{x}_i \rangle = 0\) if \(i \not= j\)

\[\begin{split} \begin{align*} \| \boldsymbol{x}_1 + \cdots + \boldsymbol{x}_m \|^2 &= \langle \boldsymbol{x}_1 + \cdots + \boldsymbol{x}_m ,\boldsymbol{x}_1 + \cdots + \boldsymbol{x}_m \rangle \\ &= \sum_{i=1}^m \sum_{j=1}^m \langle \boldsymbol{x}_i , \boldsymbol{x}_j \rangle \\ &= \sum_{i=1}^m \langle \boldsymbol{x}_i , \boldsymbol{x}_i \rangle \\ &= \| \boldsymbol{x}_1 \|^2 + \cdots + \| \boldsymbol{x}_m \|^2 \end{align*} \end{split}\]

Orthogonal Subspaces#

Let \(U_1 \subseteq \mathbb{R}^n\) and \(U_2 \subseteq \mathbb{R}^n\) be subspaces. Then \(U_1\) and \(U_2\) are orthogonal if \(\langle \boldsymbol{x}_1 , \boldsymbol{x}_2 \rangle = 0\) for all \(\boldsymbol{x}_1 \in U_1\) and \(\boldsymbol{x}_2 \in U_2\). If \(U_1\) and \(U_2\) are orthogonal subspaces, then we write \(U_1 \perp U_2\).

Let \(\{ \boldsymbol{u}_1,\dots,\boldsymbol{u}_m \}\) be a basis of a subspace \(U_1 \subseteq \mathbb{R}^n\) and let \(\{ \boldsymbol{v}_1,\dots,\boldsymbol{v}_{\ell} \}\) be a basis of a subspace \(U_2 \subseteq \mathbb{R}^n\). Then \(U_1 \perp U_2\) if and only if \(\langle \boldsymbol{u}_i , \boldsymbol{v}_j \rangle = 0\) for all \(i,j\). In other words, every \(\boldsymbol{u}_i\) in the basis of \(U_1\) is orthogonal to each \(\boldsymbol{v}_j\) in the basis of \(U_2\).

Let \(U_1 \subset \mathbb{R}^3\) and \(U_2 \subset \mathbb{R}^3\) be 2-dimensional subspaces (planes). Is it possible that \(U_1 \perp U_2\)? No!

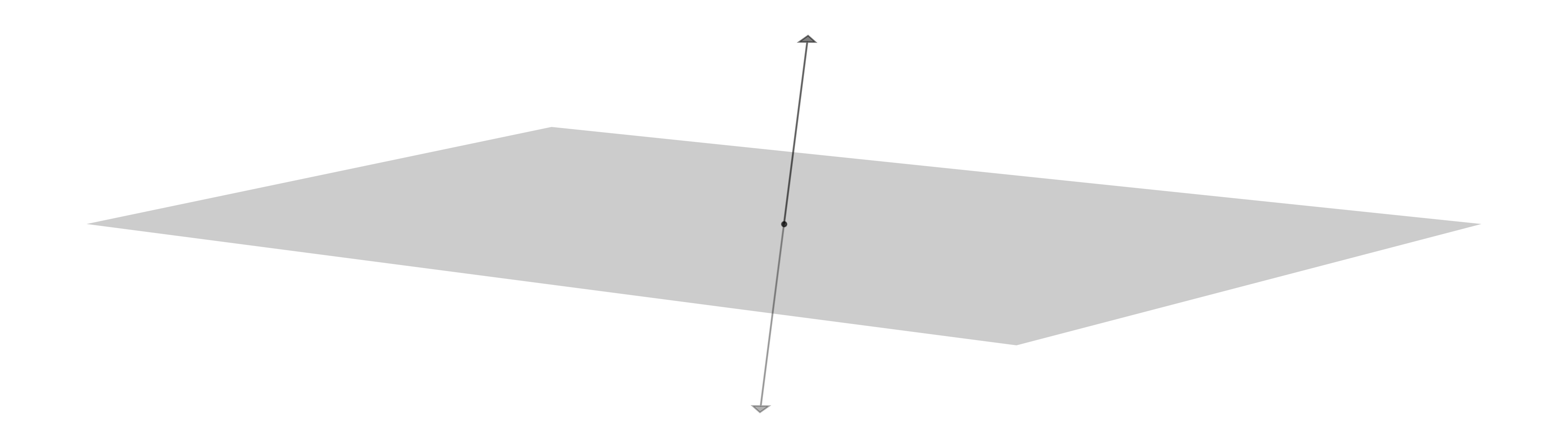
Orthogonal Complement#

Let \(U \subseteq \mathbb{R}^n\) be a subspace. The orthogonal complement of \(U\) is

\[ U^{\perp} = \{ \boldsymbol{x} \in \mathbb{R}^n : \langle \boldsymbol{x} , \boldsymbol{y} \rangle = 0 \text{ for all } \boldsymbol{y} \in U \} \]

  • If \(U \subseteq \mathbb{R}^n\) is any subspace then \(U = (U^{\perp})^{\perp}\) and also \(U \cap U^{\perp} = \{ \boldsymbol{0} \}\).

  • \(\{ \boldsymbol{0} \}^{\perp} = \mathbb{R}^n\).

Let \(U \subseteq \mathbb{R}^n\) be a subspace. Then \(U^{\perp} \subseteq \mathbb{R}^n\) is a subspace.

Proof. Let us verify that \(U^{\perp}\) satisfies the properties of a subspace.

Clearly \(\langle \boldsymbol{0} , \boldsymbol{x} \rangle = 0\) for all \(\boldsymbol{x} \in U\) therefore \(\boldsymbol{0} \in U^{\perp}\).

Let \(\boldsymbol{x}_1,\boldsymbol{x}_2 \in U^{\perp}\). Then

\[ \langle \boldsymbol{x}_1 + \boldsymbol{x}_2 , \boldsymbol{y} \rangle = \langle \boldsymbol{x}_1 , \boldsymbol{y} \rangle + \langle \boldsymbol{x}_2 , \boldsymbol{y} \rangle = 0 + 0 = 0 \]

for all \(\boldsymbol{y} \in U\) therefore \(\boldsymbol{x}_1 + \boldsymbol{x}_2 \in U^{\perp}\).

Let \(c \in \mathbb{R}\) and \(\boldsymbol{x} \in U^{\perp}\). Then

\[ \langle c\boldsymbol{x} , \boldsymbol{y} \rangle = c \langle \boldsymbol{x} , \boldsymbol{y} \rangle = c(0) = 0 \]

for all \(\boldsymbol{y} \in U\) therefore \(c \boldsymbol{x} \in U^{\perp}\).

Therefore \(U^{\perp}\) is a subspace.

Fundamental Subspaces#

Let \(A\) be a \(m \times n\) matrix. The fundamental subspaces of \(A\) are \(N(A)\), \(R(A)\), \(N(A^T)\) and \(R(A^T)\).

Let \(A\) be a \(m \times n\) matrix. Then \(N(A) = R(A^T)^{\perp}\) and \(R(A) = N(A^T)^{\perp}\).

Proof. The second equality follows from the first by replacing \(A\) with \(A^T\) therefore it is sufficient to prove \(N(A) = R(A^T)^{\perp}\). A general strategy to prove equality of sets is to show that each set contains the other therefore let us prove \(N(A) \subseteq R(A^T)^{\perp}\) and then prove the reverse \(R(A^T)^{\perp} \subseteq N(A)\).

Let \(\boldsymbol{x} \in N(A)\). Then \(A \boldsymbol{x} = \boldsymbol{0}\) therefore \(\langle A \boldsymbol{x} , \boldsymbol{y} \rangle = 0\) for all \(\boldsymbol{y} \in \mathbb{R}^m\). Using properties of the inner product we see that \(\langle \boldsymbol{x} , A^T \boldsymbol{y} \rangle = 0\) for all \(\boldsymbol{y} \in \mathbb{R}^m\) therefore \(\boldsymbol{x} \in R(A^T)^{\perp}\).

Now let \(\boldsymbol{x} \in R(A^T)^{\perp}\). Then \(\langle \boldsymbol{x} , A^T \boldsymbol{y} \rangle = 0\) and so \(\langle A \boldsymbol{x} , \boldsymbol{y} \rangle = 0\) for all \(\boldsymbol{y} \in \mathbb{R}^m\). Choose \(\boldsymbol{y} = A\boldsymbol{x} \in \mathbb{R}^m\) and then \(\langle A \boldsymbol{x} , A \boldsymbol{x} \rangle = 0\). Therefore \(\| A \boldsymbol{x} \| = 0\) and so \(A \boldsymbol{x} = \boldsymbol{0}\) and finally \(\boldsymbol{x} \in N(A)\).

Since \(N(A) \subseteq R(A^T)^{\perp}\) and \(R(A^T)^{\perp} \subseteq N(A)\) we have \(N(A) = R(A^T)^{\perp}\).

Let \(U \subseteq \mathbb{R}^n\) be a subspace. Then

\[ \dim(U) + \dim(U^{\perp}) = n \]

Proof. Let \(\dim(U) = m\) and let \(\boldsymbol{u}_1 , \dots, \boldsymbol{u}_m\) be a basis of \(U\) and define

\[\begin{split} A = \begin{bmatrix} & \boldsymbol{u}_1^T & \\ & \vdots & \\ & \boldsymbol{u}_m^T & \end{bmatrix} \end{split}\]

Then \(U = R(A^T)\) and \(U^{\perp} = R(A^T)^{\perp} = N(A)\) and we know \(\mathrm{rank}(A) = m = \dim(U)\) therefore

\[ \dim(U) + \dim(U^{\perp}) = \mathrm{rank}(A) + \dim(N(A)) = n \]

by the Rank-Nullity Theorem.

Let \(A\) be a matrix such that its LU decomposition is of the form

\[\begin{split} A = LU = \begin{bmatrix} 1 & 0 & 0 \\ * & 1 & 0 \\ * & * & 1 \end{bmatrix} \begin{bmatrix} * & * & * & * \\ 0 & * & * & * \\ 0 & 0 & * & * \end{bmatrix} \end{split}\]

where \(*\) denotes a nonzero number. Find the dimension of each subspace \(N(A)\), \(R(A)\), \(N(A^T)\) and \(R(A^T)\).

Clearly \(\dim(N(A)) = 1\) and \(\dim(R(A)) = 3\) therefore

\[ \dim(N(A^T)) = \dim(R(A)^{\perp}) = 3 - 3 = 0 \]

and

\[ \dim(R(A^T)) = \dim(N(A)^{\perp}) = 4 - 1 = 3 \]

Exercises#

Determine whether the statement is True or False.

  • Let \(U \subseteq \mathbb{R}^n\) be a subspace. If \(\boldsymbol{u} \in \mathbb{R}^n\) such that \(\boldsymbol{u} \not= 0\) then either \(\boldsymbol{u} \in U\) or \(\boldsymbol{u} \in U^{\perp}\).

  • Let \(L_1 \subset \mathbb{R}^2\) be a line through the origin. There is a unique line \(L_2 \subset \mathbb{R}^2\) through the origin such that \(L_1 \perp L_2\).

  • Let \(L_1 \subset \mathbb{R}^3\) be a line through the origin. There is a unique line \(L_2 \subset \mathbb{R}^3\) through the origin such that \(L_1 \perp L_2\).

  • Let \(U_1 \subset \mathbb{R}^4\) be a 2-dimensional subspace. There is a unique 2-dimensional subspace \(U_2 \subset \mathbb{R}^4\) through the origin such that \(U_1 \perp U_2\).

Solution

  • False

  • True

  • False

  • True

Let \(A = LU\) be the LU decomposition of \(A\). Determine whether the statement is True or False.

  • \(N(A^T) = N(U^T)\)

  • \(R(A^T) = R(U^T)\)

Solution

  • False

  • True

Determine whether the statement is True or False.

  • If \(A^TA\) is a diagonal matrix, then the columns of \(A\) are orthogonal.

  • If \(AA^T\) is a diagonal matrix, then the columns of \(A\) are orthogonal.

  • If \(A^TA\) is a diagonal matrix, then the rows of \(A\) are orthogonal.

  • If \(AA^T\) is a diagonal matrix, then the rows of \(A\) are orthogonal.

Solution

  • True

  • False

  • False

  • True

Determine whether the statement is True or False.

Let \(\boldsymbol{u}_1,\boldsymbol{u}_2,\boldsymbol{u}_3 \in \mathbb{R}^3\) be nonzero vectors. If \(\boldsymbol{u}_1\) is orthogonal to \(\boldsymbol{u}_2\), and \(\boldsymbol{u}_2\) is orthogonal to \(\boldsymbol{u}_3\) then \(\boldsymbol{u}_1\) is orthogonal to \(\boldsymbol{u}_3\).

Solution

False

Let \(A\) be a \(m \times n\) matrix and let \(\{ \boldsymbol{u}_1,\boldsymbol{u}_2 \} \subset \mathbb{R}^n\) be a basis of the nullspace \(N(A)\). Determine \(\dim(R(A^T))\) and \(\dim(N(A^T))\).

Solution

\(\dim(R(A^T)) = n-2\) and \(\dim(N(A^T)) = m-n+2\).

Let \(A\) be a \(4 \times 4\) matrix such that

\[\begin{split} A = LU = \left[ \begin{array}{rrrrrr} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 2 & 1 & 1 \end{array} \right] \left[ \begin{array}{rrrrrr} 1 & -1 & 2 & -1 \\ 0 & 1 & -3 & 4 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array} \right] \end{split}\]

Find a basis of \(N(A^T)\) and find a basis of \(R(A^T)\).

Solution
\[\begin{split} N(A^T) = \mathrm{span} \left\{ \left[ \begin{array}{r} 1 \\ -1 \\ -1 \\ 1 \end{array} \right] \right\} \hspace{10mm} R(A^T) = \mathrm{span} \left\{ \left[ \begin{array}{r} 1 \\ -1 \\ 2 \\ -1 \end{array} \right] , \left[ \begin{array}{r} 0 \\ 1 \\ -3 \\ 4 \end{array} \right] , \left[ \begin{array}{r} 0 \\ 0 \\ 0 \\ 1 \end{array} \right] \right\} \end{split}\]

Let \(A\) be a matrix such that its LU decomposition is of the form

\[\begin{split} A = LU = \begin{bmatrix} 1 & 0 & 0 \\ * & 1 & 0 \\ * & * & 1 \end{bmatrix} \begin{bmatrix} * & * & * & * \\ 0 & * & * & * \\ 0 & 0 & 0 & * \end{bmatrix} \end{split}\]

where \(*\) denotes a nonzero number. Determine the dimension of \(R(A^T)\) and the dimension of \(N(A^T)\).

Solution

\(\dim(R(A^T)) = 3\) and \(\dim(N(A^T)) = 0\)