Gradient Descent#

import numpy as np
import matplotlib.pyplot as plt

Directional Derivatives#

Let \(f(x_1,\dots,x_n)\) be a differentiable function of several variables. Use vector notation to write the function as \(f(\mathbf{x})\) where \(\mathbf{x} \in \mathbb{R}^n\). The directional derivative of \(f\) with respect to a unit vector \(\mathbf{u} \in \mathbb{R}^n\) is

\[ D_{\mathbf{u}} f(\mathbf{x}) = \left. \frac{d}{dt} \left( f(\mathbf{x} + t\mathbf{u}) \right) \, \right|_{t=0} \]

The value \(D_{\mathbf{u}} f(\mathbf{x})\) is the slope of \(f\) at \(\mathbf{x}\) in the direction \(\mathbf{u}\). Use the chain rule to compute

\[ D_{\mathbf{u}} f(\mathbf{x}) = \frac{\partial f}{\partial x_1} u_1 + \cdots + \frac{\partial f}{\partial x_n} u_n \]

See also

Check out Wikipedia: Directional Derivative for more information.

Gradient Vector#

The gradient of \(f\) is

\[ \nabla f = \left( \frac{\partial f}{\partial x_1} , \dots , \frac{\partial f}{\partial x_n} \right) \]

Therefore the directional derivative of \(f\) with respect to \(\mathbf{u} \in \mathbb{R}^n\) is the inner product

\[ D_{\mathbf{u}} f(\mathbf{x}) = \nabla f \cdot \mathbf{u} = \frac{\partial f}{\partial x_1} u_1 + \cdots + \frac{\partial f}{\partial x_n} u_n \]

This shows that the maximum value of \(D_{\mathbf{u}} f(\mathbf{x})\) occurs when \(\mathbf{u}\) points in the direction of the gradient \(\nabla f(\mathbf{x})\), and the minimum value occurs when \(\mathbf{u}\) points in the opposite direction \(-\nabla f(\mathbf{x})\).

See also

Check out Wikipedia: Gradient for more information.

Gradient Descent#

Suppose we want to minimize the function \(f(\mathbf{x})\). Choose a starting point \(\mathbf{x}_0 \in \mathbb{R}^n\). The essential observation is that the function \(f(\mathbf{x})\) decreases the fastest from the point \(\mathbf{x}_0\) in the direction \(-\nabla f(\mathbf{x_0})\). Choose a step size \(\alpha > 0\) and define the next value \(\mathbf{x}_1 = \mathbf{x}_0 - \alpha \nabla f(\mathbf{x}_0)\). Repeat the process to generate a recursive sequence of points

\[ \mathbf{x}_{k+1} = \mathbf{x}_k - \alpha \nabla f(\mathbf{x}_k) \]

The sequence \(\left\{ \mathbf{x}_k \right\}_{k=0}^{\infty}\) should converge to a point \(\mathbf{c}\) where \(f(\mathbf{c})\) is a local minimum. The algorithm is called gradient descent.

Let’s apply gradient descent to the function

\[ f(x,y) = (x - 1)^2 + 2(y + 1)^2 \]

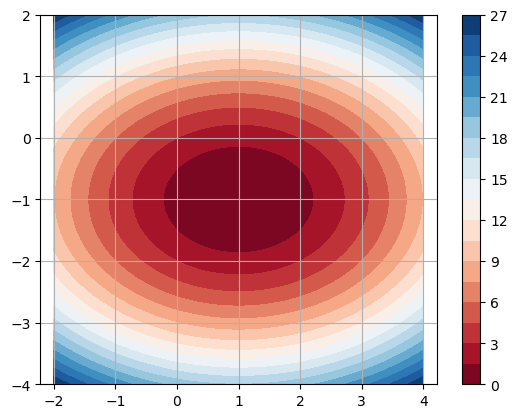
The function is a paraboloid and the global minimum occurs at \((1,-1)\). Let’s plot the level curves of \(f(x,y)\).

x = np.linspace(-2,4,50)
y = np.linspace(-4,2,50)
X,Y = np.meshgrid(x,y)
Z = (X - 1)**2 + 2*(Y + 1)**2
plt.contourf(X,Y,Z,levels=20,cmap='RdBu'), plt.colorbar()
plt.axis('equal'),plt.grid(True)
plt.show()
../../_images/b7d28d4708603d23e077e9f322141ee5ebb9f13454babb12776fbb5f586cb1ae.png

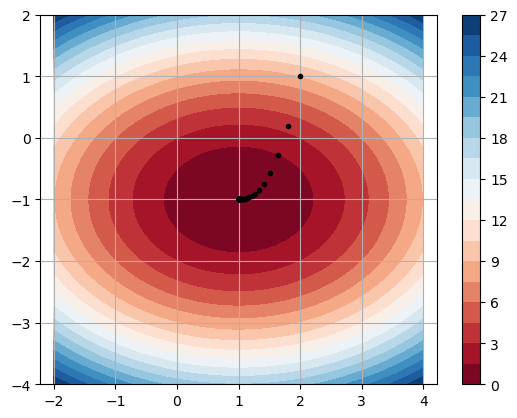
Compute the gradient

\[ \nabla f = (2x-2,4y+4) \]

and compute the sequence given by gradient descent starting from \(\mathbf{x}_0 = (2,1)\) with step size \(\alpha = 0.1\). Terminate the algorithm when \(\| \nabla f(\mathbf{x}_k) \| < 10^{-4}\).

x = np.linspace(-2,4,50)
y = np.linspace(-4,2,50)
X,Y = np.meshgrid(x,y)
Z = (X - 1)**2 + 2*(Y + 1)**2
plt.contourf(X,Y,Z,levels=20,cmap='RdBu'), plt.colorbar()

xk = np.array([2.,1.])
plt.plot(xk[0],xk[1],'k.')
alpha = 0.1
for k in range(100):
    grad = np.array([2*xk[0] - 2,4*xk[1] + 4])
    xk = xk - alpha*grad
    plt.plot(xk[0],xk[1],'k.')
    if np.linalg.norm(grad) < 1e-4:
        break

plt.axis('equal'),plt.grid(True)
plt.show()
../../_images/cfc3627b600e74d904207549bb31abacfd2d8b4882a23efec8b31c82df546925.png

Implementation#

Let’s write a function called gradient_descent which takes input parameters:

  • f is a vector function \(f(\mathbf{x})\)

  • grad is the gradient \(\nabla f(\mathbf{x})\)

  • x0 is an initial point \(\mathbf{x}_0 \in \mathbb{R}^n\)

  • alpha is the step size

  • max_iter is the maximum number of iterations

  • eps is the stopping criteria \(\| \nabla f(\mathbf{x}_k) \| < \epsilon\)

The function returns a \(m \times n\) matrix X where row \(k\) is the point

\[ \mathbf{x}_k = \mathbf{x}_{k-1} - \alpha \nabla f(\mathbf{x}_{k-1}) \]

The algorithm stops when \(\| \nabla f(\mathbf{x}_k) \| < \epsilon\) or the number of iterations exceeds max_iter. Therefore the number of rows of X is determined by the number of iterations completed. Let’s include default values alpha=0.1, max_iter=100 and eps=1e-4.

def gradient_descent(f,grad,x0,alpha=0.1,max_iter=100,eps=1e-4):
    X = np.zeros([max_iter+1,len(x0)])
    X[0,:] = x0
    for k in range(max_iter):
        xk = X[k,:]
        grad_xk = grad(xk)
        if np.linalg.norm(grad_xk) < eps:
            # Truncate the matrix X to include
            # only rows up to current index k
            X = X[:k+1,:]
            break
        X[k+1,:] = xk - alpha*grad_xk
    return X

Apply the function gradient_descent to the previous example.

f = lambda x: (x[0] - 1)**2 + 2*(x[1] + 1)**2
grad = lambda x: np.array([2*(x[0] - 1),4*(x[1] + 1)])
X = gradient_descent(f,grad,[2,1])

Check the first few iterations:

X[:5,:]

array([[ 2.    ,  1.    ],
       [ 1.8   ,  0.2   ],
       [ 1.64  , -0.28  ],
       [ 1.512 , -0.568 ],
       [ 1.4096, -0.7408]])

Check the last iterations:

X[-5:,:]

array([[ 1.00010634, -1.        ],
       [ 1.00008507, -1.        ],
       [ 1.00006806, -1.        ],
       [ 1.00005445, -1.        ],
       [ 1.00004356, -1.        ]])

Let’s see how many iterations were computed in total:

X.shape

(46, 2)

Check the norm of the gradient at the last iteration. It should be less than \(\epsilon = 10^{-4}\).

np.linalg.norm(grad(X[-1,:]))

8.711228593580309e-05

And the norm of the gradient at the second last iteration should be more than \(\epsilon = 10^{-4}\):

np.linalg.norm(grad(X[-2,:]))

0.00010889035742372364

It works as expected!

Example#

Consider the function

\[ f(x,y) = 5x^2 + 4y^2 + x^4 + 2y^4 - 10x^2y \]

Plot some levels curves of the function:

x = np.linspace(-4,4,50)
y = np.linspace(-2,3,50)
X,Y = np.meshgrid(x,y)
Z = 5*X**2 + 4*Y**2 + X**4 + 2*Y**4 - 10*X**2*Y
plt.contourf(X,Y,Z,levels=[-10,-5,-2,-1,0,1,2,5,10],cmap='RdBu'), plt.colorbar()
plt.grid(True)
plt.show()
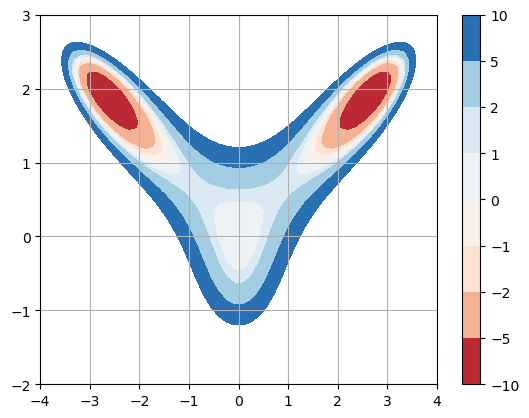
../../_images/b4f96476c41851fc0dba99813b481d6e44b384432ca2d0d843dfb45eed71bbf3.png

We see 5 critical points. Let’s approximate the local minimum near \((2.5,1.8)\). Compute the gradient

\[ \nabla f(x,y) = \left( 10x + 4x^3 - 20xy,8y + 8y^3 - 10x^2 \right) \]

Apply gradient descent to \(f(x,y)\).

f = lambda x: 5*x[0]**2 + 4*x[1]**2 + x[0]**4 + 2*x[1]**4 - 10*x[0]**2*x[1]
grad = lambda x: np.array([10*x[0] + 4*x[0]**3 - 20*x[0]*x[1], 8*x[1] + 8*x[1]**3 - 10*x[0]**2])
X = gradient_descent(f,grad,[2.5,1.8],0.01)

Inspect the first 5 points:

X[:5,:]

array([[2.5       , 1.8       ],
       [2.525     , 1.81444   ],
       [2.54485407, 1.82896844],
       [2.56201249, 1.84082887],
       [2.57638398, 1.85091924]])

And the last 5 points:

X[-5:,:]

array([[2.64421542, 1.89837822],
       [2.6442171 , 1.89837939],
       [2.64421847, 1.89838035],
       [2.64421957, 1.89838112],
       [2.64422047, 1.89838175]])

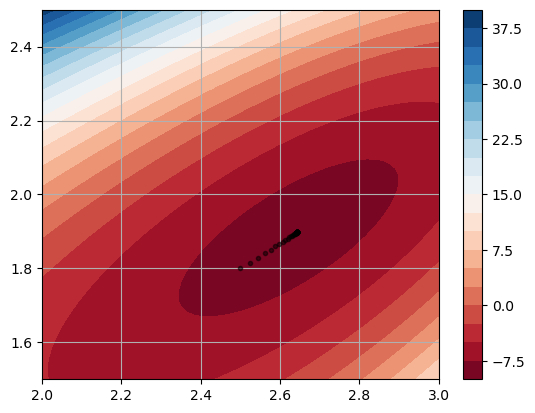
Plot all the points in the sequence to see it converge to the local minimum:

x = np.linspace(2,3,50)
y = np.linspace(1.5,2.5,50)
Xs,Ys = np.meshgrid(x,y)
Zs = 5*Xs**2 + 4*Ys**2 + Xs**4 + 2*Ys**4 - 10*Xs**2*Ys
plt.contourf(Xs,Ys,Zs,levels=20,cmap='RdBu'), plt.colorbar()
plt.plot(X[:,0],X[:,1],'k.',alpha=0.5)
plt.grid(True)
plt.show()
../../_images/b50aa7ed68f32a89ac6eec780cba695d76d1fabee3f64c7d5619203286007704.png

See also

Check out Wikipedia: Gradient Descent for more information.