Global Energy Balance#

import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate as spi

Problem Statement#

The Sun emits thermal radiation, a fraction of solar radiation is absorbed by the Earth and the rest is reflected into space, the Earth emits thermal radiation like a black body and some fraction of that thermal energy is absorbed by the atmosphere. Construct a mathematical model of the temperature of the Earth over time.

See also

Check out Mathematics and Climate > Chapter 2: Earth’s Energy Budget for more about climate models.

Variables and Parameters#

Description

Symbol

Dimensions

Type

temperature of the Earth and atmosphere

\(T\)

\(\Theta\)

dependent variable

time

\(t\)

T

independent variable

solar constant

\(S_0\)

M T-3

parameter

albedo of the Earth

\(\alpha\)

1

parameter

radius of the Earth

\(R\)

L

parameter

Stefan-Boltzmann constant

\(\sigma\)

M T-3 \(\Theta^{-4}\)

parameter

heat capacity of the Earth and atmosphere

\(C\)

M L2 T-2 \(\Theta^{-1}\)

parameter

greenhouse parameter

\(\varepsilon\)

1

parameter

Assumptions and Constraints#

  • The Earth and the atmosphere form one object with homogeneous temperature \(T\) and heat capacity \(C\)

  • \(S_0\) is constant

  • Earth emits radiation as a black body \(\sigma T^4\)

  • \(\alpha\) is constant

  • \(C\) is constant

  • \(\varepsilon\) is constant

Construction#

The rate of energy absorbed by the Earth is \(Q_{in} = (1 - \alpha) \pi R^2 S_0\) and the rate of energy emitted by the Earth is \(Q_{out} = 4 \pi R^2 \sigma \varepsilon T^4\). The energy balance equation yields

\[ C \frac{dT}{dt} = (1 - \alpha) \pi R^2 S_0 - 4 \pi R^2 \sigma \varepsilon T^4 \]

Apply the nondimensionalization procedure. Let \(t = [t] t^*\) and \(T = [T] T^*\) and make the subtitution

\[ C \frac{[T]}{[t]} \frac{dT^*}{dt^*} = (1 - \alpha) \pi R^2 S_0 - 4 \pi R^2 \sigma \varepsilon [T]^4 T^4 \]

Divide by the coefficient in \(T^4\) term

\[ \frac{C}{4 \pi R^2 \sigma \varepsilon [T]^3[t]} \frac{dT^*}{dt^*} = \frac{(1 - \alpha)S_0}{4 \sigma \varepsilon [T]^4} - T^{*4} \]

Choose values for scaling factors \([t]\) and \([T]\) to make coefficients equal to 1:

\[ [T] = \left( \frac{(1 - \alpha) S_0}{4 \sigma \varepsilon} \right)^{1/4} \hspace{10mm} [t] = \frac{C}{4 \pi R^2 \sigma \varepsilon [T]^3} = \frac{C}{4 \pi R^2 \sigma \varepsilon} \left( \frac{4 \sigma \varepsilon}{(1 - \alpha) S_0} \right)^{3/4} \]

Rewrite the system:

\[ \frac{dT^*}{dt^*} = 1 - T^{*4} \ , \ \ T^*(0) = \frac{T_0}{[T]} \]

Analysis#

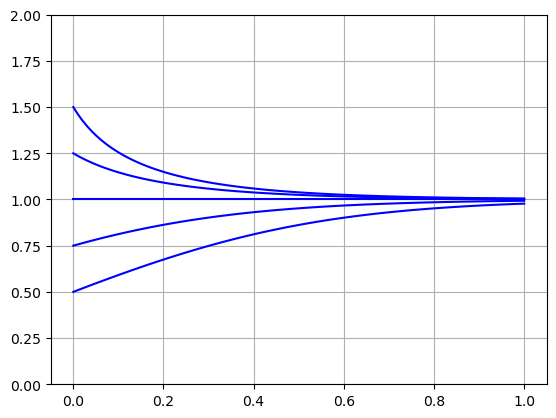
Since \(T>0\), there is only one steady state solution

\[ T^*_{\infty} = 1 \hspace{10mm} T_{\infty} = \left( \frac{(1 - \alpha) S_0}{4 \sigma \varepsilon} \right)^{1/4} \]

The steady state depends only on the solar constant \(S_0\), albedo \(\alpha\), Stefan-Boltzmann constant \(\sigma\) and greenhouse parameter \(\varepsilon \). The parameters \(C\) and \(R\) only change the time scale \([t]\).

f = lambda T,t: 1 - T**4
t = np.linspace(0,1,100)

for T0 in [0.5,0.75,1.0,1.25,1.5]:
    T = spi.odeint(f,T0,t)
    plt.plot(t,T,'b')

plt.ylim([0,2]),plt.grid(True)
plt.show()
../../_images/09f16fef92c12761717ab2a61b7edc2ca0b2612b82ad7a43c31312b38cc9592a.png