Uniform Distribution

Uniform Distribution#

import numpy as np
import matplotlib.pyplot as plt

The uniform distribution (with parameters \(a < b\)) is given by the probability density function

\[\begin{split} f(x) = \left\{ \begin{array}{ccc} \displaystyle \frac{1}{b-a} & , & a \le x \le b \\ 0 & , & \text{otherwise} \end{array} \right. \end{split}\]

We denote the uniform distribution by \(U(a,b)\). The mean and variance are given by

\[ \mu = \frac{b+a}{2} \hspace{1in} \sigma^2 = \frac{(b-a)^2}{12} \]

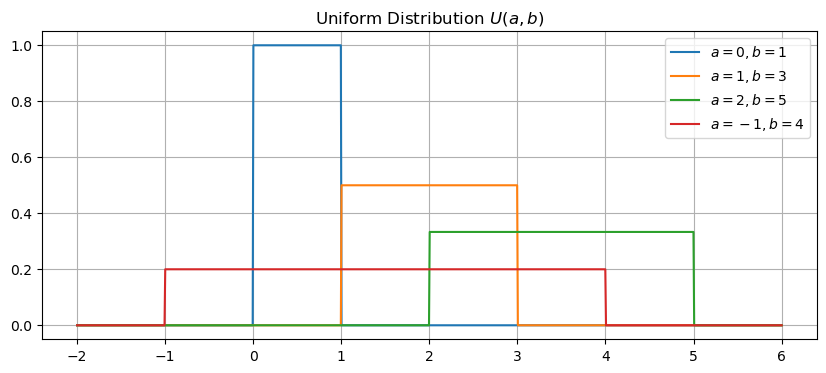
Let’s plot the uniform distrbution for different values of \(a\) and \(b\). Use the function np.heaviside to construct the probability density function (see documentation).

plt.figure(figsize=(10,4))
x = np.linspace(-2,6,1000)
uniform = lambda x,a,b: 1/(b-a)*(np.heaviside(x-a,1) - np.heaviside(x-b,1))
for a,b in [(0,1),(1,3),(2,5),(-1,4)]:
    y = uniform(x,a,b)
    plt.plot(x,y)
plt.title('Uniform Distribution $U(a,b)$')
plt.legend(['$a=0,b=1$','$a=1,b=3$','$a=2,b=5$','$a=-1,b=4$'])
plt.grid(True)
plt.show()

../../_images/02a2cb1b463eb5206831834f8ddad3046cd929510a8a6524ee0815d99e8ac4e5.png