Chemical Kinetics#

import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate as spi

Stoichiometry#

Stoichiometry is the quantitative study of reactants and products in chemical reactions. Reactants and products are molecules which consist of a combination of atoms of chemical elements. For example, water is a molecule composed of two hydrogen atoms and one oxygen atom and is written as \(H_2O\). We represent a chemical reaction by a stoichiometric equation which lists the reactants on the left and the products on the right along with their stoichiometric coefficients which describes the number of each molecule involed in the reaction. For eaxmple, the combustion reaction of methane is given by the equation

\[ CH_4 + 2 O_2 \rightarrow CO_2 + 2 H_2O \]

The equation states that one methane molecule (\(CH_4\)) reacts with two oxygen molecules (\(O_2\)) to produce one carbon dioxide molecule (\(CO_2\)) and two water molecules (\(H_2O\)).

Stoichiometric equations must be balanced according to the law of conservation of mass. This means that the total number of atoms of each element in the reactants must equal the total in the products. For example, in the equation above, we see that there are four oxygen atoms, one carbon atom and four hydrogen atoms on both sides of the equation.

See also

Check out Wikipedia: Stoichiometry for more information.

Concentration and Reaction Rate#

Molar concentration is the amount of a substance per unit volume and has dimensions NL-3. We use molar concentration exclusively when studying chemical reactions and so we simply say concentration to mean molar concentration.

The reaction rate of a chemical reaction is the concentration of reactant transformed into product per unit time. The reaction rate has dimensions NL-3T-1.

Law of Mass Action#

The law of mass action states that the reaction rate of a chemical reaction is directly proportional to the product of the concentrations of the reactants. In other words, if a reaction is given by the stoichiometric equation

\[ c_1 R_1 + \cdots + c_n R_n \rightarrow P \]

then the reaction rate is

\[ k R_1^{c_1} \cdots R_n^{c_n} \]

where we use the notation \(R_1,\dots,R_n\) to denote the concentrations of the reactants and \(k\) is the reaction coefficient. Note that the reaction coefficient \(k\) has dimensions (NL-3)1 - rT-1 where \(r = c_1 + \cdots + c_n\). We use the following notation to denote a chemical reaction with coefficient \(k\):

\[ c_1 R_1 + \cdots + c_n R_n \overset{k}{\rightarrow} P \]

The law of mass action gives rise to a differential equation for each reactant

\[ \frac{dR_i}{dt} = c_i k R_1^{c_1} \cdots R_n^{c_n} \ , \ \ i=1,\dots,n \]

See also

Check out A Primer on Mathematical Models in Biology > Chapter 2: Introduction to Biochemical Kinetics for more examples and information.

Enzyme Kinetics#

Enzymes are proteins that act as biological catalysts by accelerating chemical reactions. Suppose an enzyme \(E\) catalyzes the transformation of a substrate \(S\) into a product \(P\)

\[ E + S \underset{k_{-1}}{\overset{k_1}{\rightleftharpoons}} C \overset{k_2}{\rightarrow} E + P \]

The diagram above states that:

  • \(E\) and \(S\) combine with rate coefficient \(k_1\) to produce the enzyme-substrate complex \(C\)

  • \(C\) is reversible and decomposes into \(E\) and \(S\) with rate coefficient \(k_{-1}\)

  • \(C\) transforms back into the enzyme \(E\) and product \(P\) with rate coefficient \(k_2\)

Apply the law of mass action to derive the system of differential equations for the concentrations of each molecule:

\[\begin{split} \begin{align*} \frac{dE}{dt} &= - k_1 ES + k_{-1} C + k_2 C \\ \frac{dS}{dt} &= -k_1 ES + k_{-1} C \\ \frac{dC}{dt} &= k_1 ES - k_{-1} C - k_2 C\\ \frac{dP}{dt} &= k_2 C \end{align*} \end{split}\]

Apply the nondimensionalization procedure. Let \(E = [E]E^*\), \(S = [S]S^*\), \(C = [C]C^*\) and \(P = [P]P^*\) and make the substitution:

\[\begin{split} \begin{align*} \frac{[E]}{[t]} \frac{dE^*}{dt^*} &= - k_1 [E][S]E^*S^* + \left( k_{-1} + k_2 \right)[C] C^* \\ \frac{[S]}{[t]} \frac{dS^*}{dt^*} &= -k_1 [E][S]E^*S^* + k_{-1}[C]C^* \\ \frac{[C]}{[t]} \frac{dC^*}{dt^*} &= k_1 [E][S]E^*S^* - \left( k_{-1} + k_2 \right) [C]C^* \\ \frac{[P]}{[t]} \frac{dP^*}{dt^*} &= k_2[C]C^* \end{align*} \end{split}\]

Divide by the derivative term and write

\[\begin{split} \begin{align*} \frac{dE^*}{dt^*} &= - k_1 [t][S]E^*S^* + \left( k_{-1} + k_2 \right) \frac{[C][t]}{[E]}C^* \\ \frac{dS^*}{dt^*} &= -k_1 [t][E]E^*S^* + \frac{k_{-1}[C][t]}{[S]} C^* \\ \frac{dC^*}{dt^*} &= \frac{k_1 [E][S][t]}{[C]}E^*S^* - \left( k_{-1} + k_2 \right) [t]C^* \\ \frac{dP^*}{dt^*} &= \frac{k_2[C][t]}{[P]}C^* \end{align*} \end{split}\]

Choose the scaling factors

\[ [t] = \frac{1}{k_{-1} + k_2} \hspace{20mm} [E] = [S] = [C] = \frac{k_{-1} + k_2}{k_1} \hspace{20mm} [P] = \frac{k_2}{k_1} \]

and write

\[\begin{split} \begin{align*} \frac{dE^*}{dt^*} &= -E^*S^* + C^* \\ \frac{dS^*}{dt^*} &= -E^*S^* + \kappa \, C^* \\ \frac{dC^*}{dt^*} &= E^*S^* - C^* \\ \frac{dP^*}{dt^*} &= C^* \end{align*} \end{split}\]

where \(\kappa = \frac{k_{-1}}{k_{-1} + k_2}\).

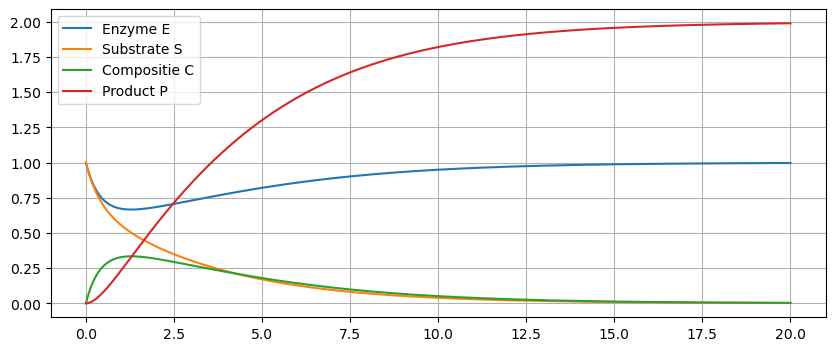
Plot some solutions:

k = 1/2
# E = u[0], S = u[1], C = u[2], P = u[3]
f = lambda u,t: np.array([-u[0]*u[1] + u[2],-u[0]*u[1] + k*u[2],u[0]*u[1] - u[2],u[2]])
u0 = [1,1,0,0]
t = np.linspace(0,20,500)
u = spi.odeint(f,u0,t)
plt.figure(figsize=(10,4))
plt.plot(t,u[:,0],t,u[:,1],t,u[:,2],t,u[:,3])
plt.legend(['Enzyme E','Substrate S','Compositie C','Product P']), plt.grid(True)
plt.show()
../../_images/33ef6cc4a1cc5b6cd61fed7fce0c79140f2c14662816c39b5707ea821b5dbedf.png